Enhancing spatial domain detection in spatial transcriptomics with EnSDD
先用chatgpt提炼一下要点:
# 论文要点提炼:《Enhancing Spatial Domain Detection in Spatial Transcriptomics with EnSDD》
# 1. 研究背景
- 空间转录组学(Spatial Transcriptomics, SRT)帮助理解器官功能和组织微环境,但空间域(spatial domains)的准确识别仍是挑战。
- 现有的空间域检测方法(如 BayesSpace、GraphST、STAGATE 等)存在局限,如忽略组织形态信息,或受数据复杂性影响效果不稳定。
- 传统方法难以选择最佳的检测方法,因此需要集成学习(ensemble learning)策略来整合多种方法的结果。
# 2. 研究目标
- 提出 EnSDD (Ensemble-learning for Spatial Domain Detection),整合 8 种先进的空间域检测方法,并使用 动态加权机制 来优化每种方法的贡献。
- 该方法可 自动评估各方法的性能,无需依赖人工标注(ground truth)。
- EnSDD 还能够识别 特定空间域的差异表达基因(SVGs) 和 细胞类型空间分布,提供更深层次的组织异质性见解。
# 3. 方法创新
- 动态加权机制:EnSDD 通过优化模型自适应地分配各基方法的权重,并生成一个 共识相似度矩阵(consensus similarity matrix)。
- 自动调整聚类参数:采用 Louvain 算法的自适应分辨率调整策略,确保聚类结果的优化。
- 集成 8 种方法:包括 BayesSpace、DR-SC、GraphST、STAGATE、SpaGCN、stLearn、SiGra 和 spaVAE,结合空间坐标、基因表达数据和组织形态图像进行聚类分析。
# 4. 主要实验与结果
# (1) 在人类大脑 DLPFC 数据集上的表现
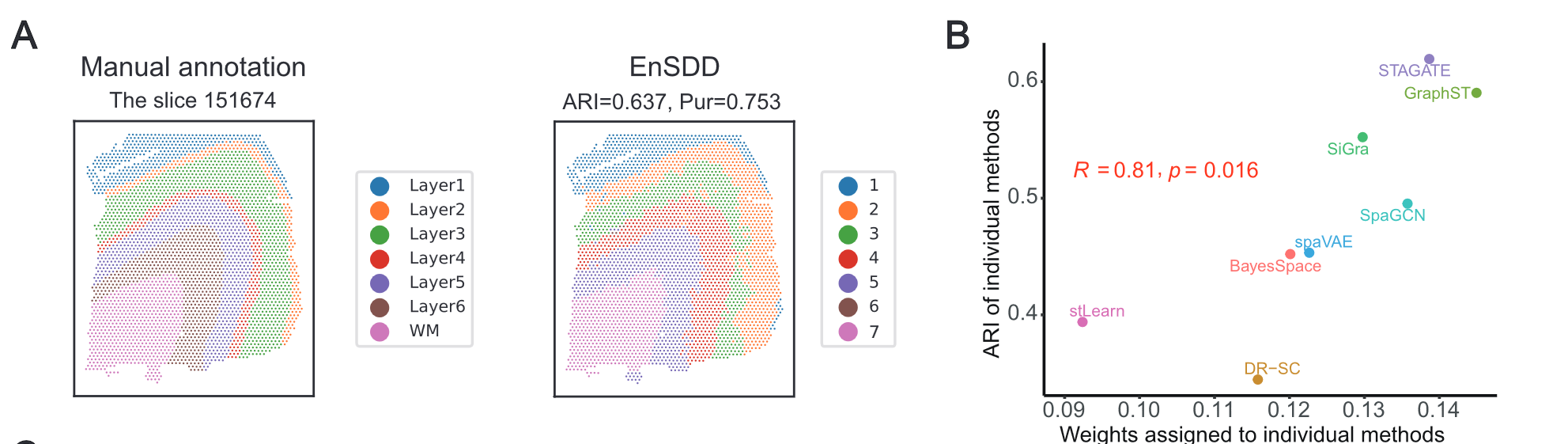
- EnSDD 在 12 个人类 DLPFC(前额叶皮层)切片上进行测试,结果显示:
- 在大多数切片上表现最佳,准确划分了不同皮层层次。
- 以 调整兰德指数(ARI)= 0.637 和 纯度(Purity)= 0.753 在部分切片中取得最高聚类准确度。
- 与人工标注相比,部分区域的划分更细(如 Layer 3 进一步被细分),表明 EnSDD 具有较强的发现新结构的能力。
# (2) 在小鼠大脑数据集上的验证
- 采用 Allen Brain Atlas 作为参考标准,EnSDD 成功识别出 大脑皮层 6 层结构、海马 CA1 结构、齿状回(DG) 等重要区域。
- 相比其他方法更稳定,即使调整聚类数量,EnSDD 仍能保持空间域的连贯性,而其他方法如 BayesSpace、stLearn 在某些情况下生成不连续的区域。
# (3) 在癌症组织(乳腺癌、前列腺癌和卵巢癌)上的应用
乳腺癌:
- EnSDD 识别出不同的 肿瘤区域(IDC、DCIS/LCIS) 及肿瘤边缘的细微异质性。
- 通过差异基因分析,发现了 IDC_5 区域的关键基因(如 CSTA、FAM234B、HEBP1),揭示了潜在的肿瘤进展机制。
- 肿瘤微环境分析 显示,IDC 5 区域的 巨噬细胞和树突状细胞 含量较高,可能与肿瘤免疫逃逸相关。
前列腺癌:
- 成功识别 肿瘤区域 和 肿瘤边界(ecotone),相比其他方法,EnSDD 更精确地区分了肿瘤与周围组织的异质性。
- 发现 KLK3、TP63、ATG9B 等基因在肿瘤边缘具有显著表达变化,可能影响前列腺癌的进展。
卵巢癌:
- EnSDD 成功检测到 肿瘤 - 基质交界区(tumor-stroma interface),揭示了肿瘤微环境的复杂性。
- 识别的关键基因 SFRP4、IGKN、THBS1 可能与肿瘤侵袭能力相关,提示 EnSDD 可用于肿瘤生物标志物的发现。
# 5. 贡献与未来展望
- EnSDD 比单一方法更稳定,可自动评估不同方法的贡献,适用于 不同类型的组织结构。
- 未来可扩展至 多切片分析(multi-slice analysis),探索组织在多个切片间的连续性。
- 结合外部参考数据 可能进一步提升 EnSDD 在未知数据集上的适用性。
# 总结
这篇论文提出了一种 基于集成学习的空间域检测方法 EnSDD,在多个数据集上表现优异,能更准确地识别 空间域结构、差异基因和细胞类型分布,并适用于 复杂组织结构及肿瘤微环境研究,为空间转录组学分析提供了新的工具。
# two main challenges:
- differing base methods may produce varying numbers and types of spatial doamins, complicating the integration of their results
- the performance of methods can vary across datasets, making it difficult to automatically assess and incorporate method performance into the ensemble process.
# EnSDD(Ensemble-learning for Spatial Domain Detection) offers several advantages:
- EnSDD adaptively assigns weights to similarity matrices generated by base methods, learning the complete similarity between spots
- the weights assigned by EnSDD provide a reliable metric for evaluating the performance of base SDD methods without requiring ground truth.
- EnSDD offers a comprehensive framework for exploring tissue spatial organization, including the identification of spatial domains, determination of domain-specific SVGs, and inference of cell type distribution
- it includes well-documented tutorials and an interative platform to facilitate implementation and visualization.
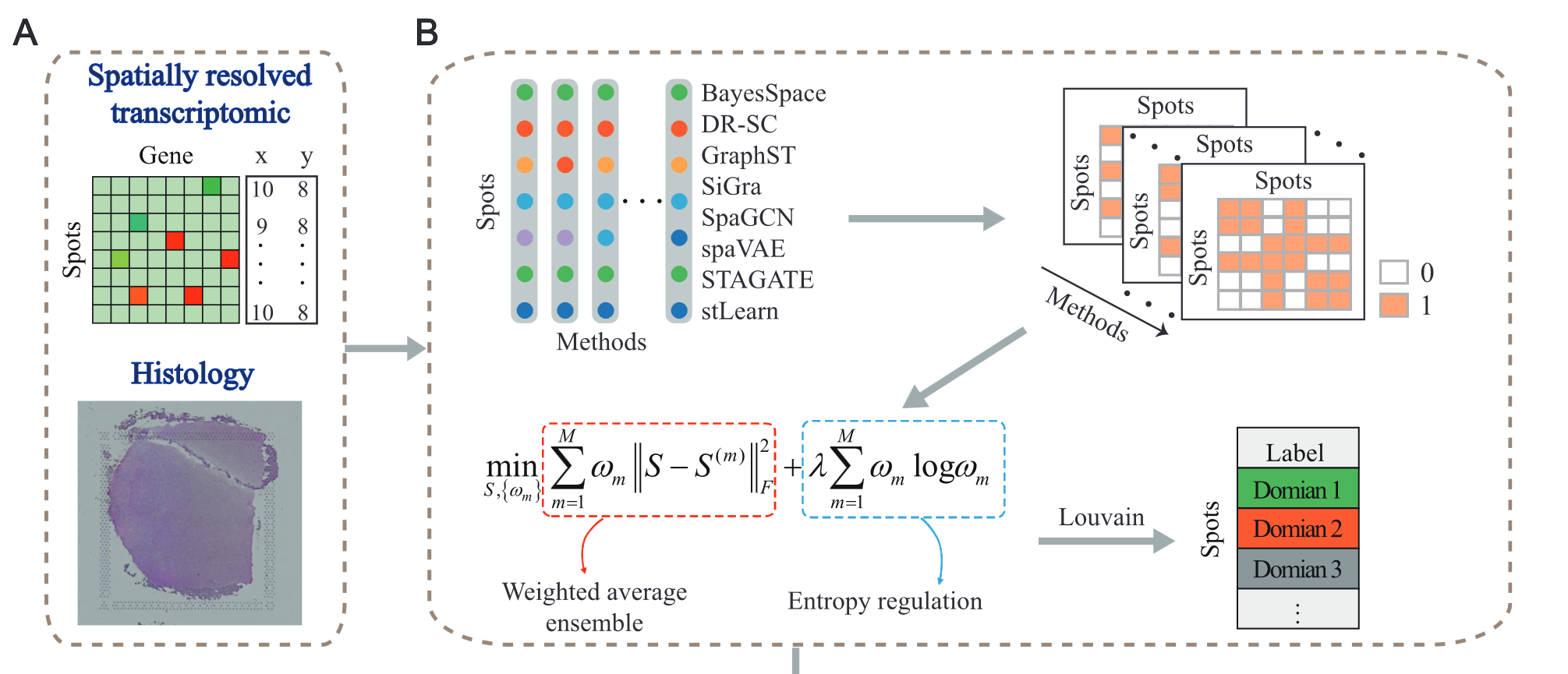
大概概括一下整个流程:
首先将各种各样的数据输入进模型,这个模型下的 8 个 base methods 会生成结果,然后右图的那个代表 0,1 的矩阵的意思是两个 spot 之间是否属于一个 cluster,通过使用这些矩阵,EnSDD 会运用一个优化模型去决定最终的 similarity matrix,并且把可自适应的权重分给 base method,然后这些权重便成为了衡量 base method 的方式。最终 EnSDD 运用 Louvain 算法去最终决定 spatial domains。
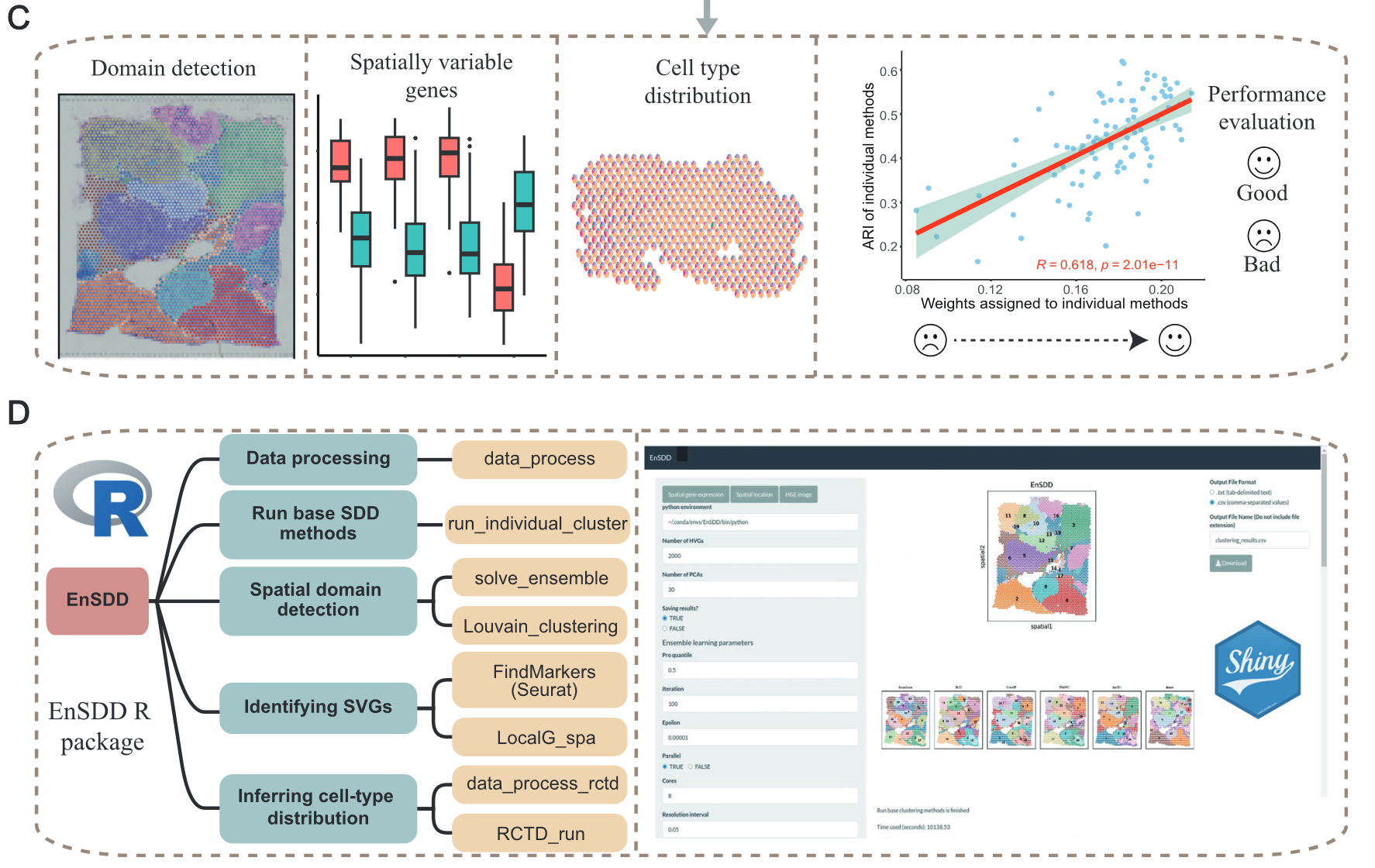
EnSDD offers two approaches for identifying SVGs:
- one involves detecting domain-specific differentially expressed genes(DEGs)
- other identifies gene with expression patterns with expression patterns correlated to spatial locations
在科研中,gold standard 指的是被广泛接受、被认为是最准确和权威的 “真值” 或参考数据,通常由专家通过严格的人工注释获得。例如,在前列腺癌数据中,病理学家提供的肿瘤和肿瘤边缘区域标注就被视为 gold standard,用来评估算法的准确性。而 silver standard 则是指在没有绝对完美的 gold standard 时使用的参考数据,这类数据虽然不是最完美的,但仍能作为一个有用的基准来评价方法的表现。例如,在某些小鼠大脑数据中,Allen Brain Atlas 被用作 silver standard。总体来说,gold standard 是最理想的标准,而 silver standard 则是在实际条件下的一个次优但可接受的替代。
针对乳腺癌数据板块的对于 cell proportion 的分析可以借鉴一下
其它的集成学习方法
STAMarker 和 SC3 都是利用集成学习思想的聚类方法,但它们应用的场景和侧重点有所不同:
SC3 是一种用于单细胞 RNA 测序(scRNA-seq)数据聚类的方法。它通过整合多个聚类结果得到多个二元相似度矩阵,然后利用层次聚类生成最终的细胞分类结果。这种方法能够整合不同算法的信息,从而获得更稳健的聚类结果。
STAMarker 则主要用于空间转录组学数据中的空间域检测。它计算不同聚类结果中任意两个空间点共同归入同一空间域的比例,形成一个连接矩阵,再利用层次聚类或 Louvain 算法来进行标签分配,从而识别出具有生物学意义的空间域。
这两种方法都是通过集成多种聚类结果来提高整体的准确性和稳健性,但 SC3 更侧重于单细胞数据的细胞分类,而 STAMarker 则专注于空间域的划分。
# Methods 部分
在 Methods 部分,作者主要介绍了 EnSDD 模型的构建和求解方法,其中核心在于如何将来自多个基础空间域检测方法(如 BayesSpace、DR-SC、GraphST、STAGATE、SpaGCN、stLearn、SiGra 和 spaVAE)得到的二值相似矩阵进行加权融合,进而生成一个共识相似矩阵 S,从而指导后续的空间域划分。下面详细说明公式部分的主要内容:
# 1. 二值相似矩阵构造
对于每个基础方法 m(m = 1, …, M,默认 M = 8),根据其聚类结果构造一个二值相似矩阵 。具体来说,对于任意两个点 i 和 j,如果它们在方法 m 中被划分到同一聚类,则 ;否则为 0。这一步的目的在于将各方法的聚类结果以矩阵的形式表达出来。
# 2. 优化模型与加权融合公式
为了整合这些基础方法得到的相似矩阵,作者提出了如下优化问题:
\begin{align} \min_{S, \{\omega_m\}} \quad \sum_{m=1}^{M} \omega_m \|S - S^{(m)}\|_F^2 + \lambda \sum_{m=1}^{M} \omega_m \log \omega_m \end{align} \begin{align} \text{subject to} \quad \sum_{m=1}^{M} \omega_m = 1, \quad \omega_m \geq 0 \quad (m=1,\ldots,M) \end{align}其中:
- S 是待学习的共识相似矩阵。
- S^(m) 是第 m 个基础方法构造的二值相似矩阵。
- 表示矩阵的 Frobenius 范数的平方,即衡量两个矩阵之间的欧氏距离。
- 是分配给第 m 个基础方法的权重,这些权重反映了每个方法在当前数据集上的表现好坏。直观上,表现较好的方法会获得较大的权重,使得共识矩阵 S 与该方法的 S^(m) 更加接近。
- 是调节负熵正则化项的参数。正则化项 的引入能够防止权重过于集中在某一个方法上,从而避免过拟合。
公式解析:
第一项:
这部分计算了共识矩阵 S 与每个基础方法的相似矩阵之间的加权差异。对每个方法 m,距离越小表明 S 更接近于该方法的结果,且这个距离由相应的权重 加权求和。第二项:
这是一个负熵正则化项,它在优化过程中会鼓励权重分布更加平滑,防止某个方法的权重过大。这里的 λ 控制了正则化的强度,当 λ 较大时,权重分布会更加均衡;当 λ 较小时,可能会倾向于将大部分权重赋予表现最好的方法。约束条件: 且
这保证了所有权重构成一个概率分布,即所有权重之和为 1,并且每个权重都是非负的。
作者采用坐标下降算法来求解这个优化问题,即交替优化 S 与 的值。最终得到的共识相似矩阵 S 能够更准确地反映各基础方法综合后的空间点相似性,同时各 也可作为评估各基础方法在特定数据集上表现的指标。
第一项偏导
这是一个经典的带权 Frobenius 距离最小化问题,常出现在集成学习、矩阵逼近或多视图聚类中。你问的是下面这个优化目标:
# 📌 优化问题
\begin{equation} \min_{S, \{\omega_m\}} \quad \sum_{m=1}^{M} \omega_m \|S - S^{(m)}\|_F^2 \end{equation}其中:
- 是你要求解的集成矩阵
- 是每个 base 矩阵的权重(你暂时是常数或已知的情况下求偏导)
- 是第 个给定的相似度矩阵
- 表示 Frobenius 范数
# 🎯 要求:
你现在是想对 求偏导数,也就是:
\begin{equation} \frac{\partial}{\partial S} \left( \sum_{m=1}^{M} \omega_m \|S - S^{(m)}\|_F^2 \right) \end{equation}# 🧮 计算步骤
我们知道:
\begin{equation} \|A\|_F^2 = \sum_{i,j} A_{ij}^2 = \operatorname{Tr}(A^\top A) \end{equation}所以每一项:
\begin{equation} \|S - S^{(m)}\|_F^2 = \operatorname{Tr}\left((S - S^{(m)})^\top (S - S^{(m)})\right) \end{equation}对 求导的标准结果是:
\begin{equation} \frac{\partial}{\partial S} \|S - S^{(m)}\|_F^2 = 2(S - S^{(m)}) \end{equation}# 🧾 于是整体偏导为:
\begin{equation} \frac{\partial}{\partial S} \sum_{m=1}^{M} \omega_m \|S - S^{(m)}\|_F^2 = \sum_{m=1}^{M} \omega_m \cdot 2(S - S^{(m)}) = 2 \sum_{m=1}^{M} \omega_m (S - S^{(m)}) \end{equation}# ✅ 最终结果:
\begin{equation} \frac{\partial}{\partial S} \left( \sum_{m=1}^{M} \omega_m \|S - S^{(m)}\|_F^2 \right) = 2 \sum_{m=1}^{M} \omega_m (S - S^{(m)}) \end{equation}# 💡 如果你要最小化它,只需让偏导为 0:
\begin{equation} \sum_{m=1}^{M} \omega_m (S - S^{(m)}) = 0 \quad \Rightarrow \quad S = \sum_{m=1}^{M} \omega_m S^{(m)} \end{equation}也就是说,最优解 是所有矩阵的 加权平均!
需要我帮你把这推导写成 LaTeX 公式或加到你自己的代码推导里也可以继续说哈~
第二项偏导
太好了!你这个问题非常经典,咱们现在就来一步步推导怎么用 Lagrange 乘子法(Lagrange multipliers)来求解权重 的最优解。
# 🔢 你给的目标函数是:
\begin{equation} \min_{\{ \omega_m \}} \quad \sum_{m=1}^M \omega_m \| S - S^{(m)} \|_F^2 + \lambda \sum_{m=1}^M \omega_m \log \omega_m \end{equation}带有约束:
\begin{equation} \sum_{m=1}^M \omega_m = 1, \quad \omega_m \geq 0 \end{equation}其中 是固定的(或者在交替优化里暂时固定),所以我们只针对 来优化。
# ✏️ 第一步:写出 Lagrangian 拉格朗日函数
为了处理约束 ,引入拉格朗日乘子 ,构造:
\begin{equation} \mathcal{L}(\omega_1, \ldots, \omega_M, \mu) = \sum_{m=1}^M \omega_m \| S - S^{(m)} \|_F^2 + \lambda \sum_{m=1}^M \omega_m \log \omega_m - \mu \left( \sum_{m=1}^M \omega_m - 1 \right) \end{equation}# 🧮 第二步:对每个 求偏导数
我们令每个偏导为 0:
\begin{equation} \frac{\partial \mathcal{L}}{\partial \omega_m} = \| S - S^{(m)} \|_F^2 + \lambda(1 + \log \omega_m) - \mu = 0 \end{equation}整理一下:
\begin{equation} \lambda \log \omega_m = \mu - \lambda - \| S - S^{(m)} \|_F^2 \end{equation}再除以 并指数两边:
\begin{equation} \log \omega_m = \frac{\mu - \lambda - \| S - S^{(m)} \|_F^2}{\lambda} \Rightarrow \omega_m = \exp\left( \frac{\mu - \lambda - \| S - S^{(m)} \|_F^2}{\lambda} \right) \end{equation}整理一下:
\begin{equation} \omega_m = C \cdot \exp\left( -\frac{1}{\lambda} \| S - S^{(m)} \|_F^2 \right) \end{equation}其中 是一个所有 的共同常数。
# ✅ 第三步:用约束条件求出
由于所有 要满足:
\begin{equation} \sum_{m=1}^M \omega_m = 1 \end{equation}我们将上面形式代入得:
\begin{equation} \sum_{m=1}^M C \cdot \exp\left( -\frac{1}{\lambda} \| S - S^{(m)} \|_F^2 \right) = 1 \Rightarrow C = \frac{1}{\sum_{m=1}^M \exp\left( -\frac{1}{\lambda} \| S - S^{(m)} \|_F^2 \right)} \end{equation}# 🎉 最终结果:
\begin{equation} \boxed{ \omega_m = \frac{ \exp\left( -\frac{1}{\lambda} \| S - S^{(m)} \|_F^2 \right) }{ \sum_{j=1}^M \exp\left( -\frac{1}{\lambda} \| S - S^{(j)} \|_F^2 \right) } } \end{equation}这其实就是一个 softmax 形式!每个 是对 的一个相似度评分(用负的距离衡量),用 softmax 来归一化。
# 📌 补充说明
- 如果 :权重趋向于 “winner takes all”(只选最小误差的那个)
- 如果 :所有权重接近均匀平均
- 这个方法就是你之前代码中那个权重更新公式的数学基础
如果你想我也可以帮你推对 的梯度,或者画图解释这个 softmax 权重的直觉含义 😄 想继续哪一块?
当然可以!我们就专注于这一步:如何对每个 求偏导数。
你给的函数是:
\begin{equation} \mathcal{L}(\omega_1, \ldots, \omega_M, \mu) = \sum_{m=1}^M \omega_m \|S - S^{(m)}\|_F^2 + \lambda \sum_{m=1}^M \omega_m \log \omega_m - \mu \left( \sum_{m=1}^M \omega_m - 1 \right) \end{equation}我们现在只关注其中一个 ,要对它求偏导数。
# 🔍 拆开看,(\mathcal {L}) 对于单个 (\omega_m) 是:
选定一个 ,(\mathcal {L}$ 中关于 的部分是:
\begin{equation} \omega_m \|S - S^{(m)}\|_F^2 + \lambda \omega_m \log \omega_m - \mu \omega_m \end{equation}这是三项:
- 线性项:
- 熵正则项:
- 约束乘子项:
# 🧮 逐项对 求导
# 第一项:
\begin{equation} \frac{\partial}{\partial \omega_m} \left( \omega_m \cdot \|S - S^{(m)}\|_F^2 \right) = \|S - S^{(m)}\|_F^2 \end{equation}这是因为 是常数,对 直接是乘法。
# 第二项(关键点):
\begin{equation} \frac{\partial}{\partial \omega_m} \left( \omega_m \log \omega_m \right) \end{equation}我们来慢慢推一下这个常见表达式的导数:
令:
\begin{equation} f(\omega) = \omega \log \omega \end{equation}用乘积法则:
\begin{equation} f'(\omega) = \frac{d}{d\omega} \omega \cdot \log \omega = 1 \cdot \log \omega + \omega \cdot \frac{1}{\omega} = \log \omega + 1 \end{equation}所以:
\begin{equation} \frac{\partial}{\partial \omega_m} \left( \lambda \omega_m \log \omega_m \right) = \lambda (\log \omega_m + 1) \end{equation}# 第三项:
\begin{equation} \frac{\partial}{\partial \omega_m} (-\mu \omega_m) = -\mu \end{equation}# 🔚 把三项加起来,得到偏导:
\begin{equation} \frac{\partial \mathcal{L}}{\partial \omega_m} = \|S - S^{(m)}\|_F^2 + \lambda (\log \omega_m + 1) - \mu \end{equation}然后我们令偏导为 0,得到最优条件:
\begin{equation} \|S - S^{(m)}\|_F^2 + \lambda (\log \omega_m + 1) - \mu = 0 \end{equation}就是我们之前推导的式子啦!
# 🎯 总结一下你学到什么:
- 对 求导是 (这是熵类正则常见的导数)
- 在加权平均里用 softmax,其实就是从这个偏导数出发
- 拉格朗日乘子 用于处理总和为 1 的约束
如果你想,我还可以做成一张「可视化推导卡片」,更方便你日后复习!要不要试试?
# 3. 空间域的划分
得到共识相似矩阵 S 后,EnSDD 进一步使用 Louvain 算法进行社区发现(即聚类),并通过自适应分辨率调整(利用二分搜索确定最佳分辨率参数),将 SRT 数据中的点划分为不同的空间域。这样既能保证空间域的连贯性,也能在预设的聚类数下获得较优的划分结果。
# 4. 后续分析
在共识相似矩阵和空间域划分的基础上,EnSDD 还进一步进行:
- 差异表达基因(SVGs)的识别:利用 Wilcoxon 检验比较各空间域之间的基因表达水平,识别出在特定空间域中具有显著表达变化的基因。
- 局部空间自相关分析:采用 Local Getis and Ord’s Gi 统计量,评估基因表达在局部空间内的聚集或分散趋势,从而揭示基因的空间自相关特征。
SA
# 空间自相关(Spatial Auto-correlation, SA)的使用
在 EnSDD 研究中,空间自相关用于分析 基因表达在空间上的依赖性,即在组织切片中,基因的表达水平是否在空间上呈现聚集或分散模式。这有助于识别 空间可变基因(SVGs, Spatially Variable Genes),即在特定空间区域内具有特定表达模式的基因。
# 1. 什么是空间自相关?
空间自相关(SA)是指某一变量(这里是基因表达水平)在空间上的分布模式是否表现出 相似性或相关性。一般来说:
- 正空间自相关(Positive SA):相邻位置的基因表达水平相似,呈现聚集模式。例如,在大脑皮层某个区域,如果某个基因的表达量高,其周围位置的表达量也较高。
- 负空间自相关(Negative SA):相邻位置的基因表达水平相反,呈现分散模式。例如,某些基因在神经组织和周围支持细胞中表现出相反的表达模式。
EnSDD 采用 Local Getis and Ord’s Gi 统计量 来定量衡量某个基因在局部空间中的自相关性。
# 2. Local Getis and Ord’s 统计量
EnSDD 通过 Local Getis and Ord’s 统计量来评估基因表达的空间聚集性。这一统计量用于衡量每个基因在空间中的局部自相关性,数学表达如下:
\begin{align} G_i(k) = \frac{\sum\limits_{j} c_{ij}(k) x_j - V_i \mu}{\sigma \left\{(n-1)B_{1i} - V_i^2\right\}^{1/2}}, \quad i \neq j \end{align}其中:
- :第 个空间点的基因表达水平。
- , :所有空间点(去除第 个点)的基因表达的均值和标准差。
- :空间权重矩阵,表示空间点 与 之间的距离权重(例如,最近的 k 个点的权重为 1,其余为 0)。
- :第 个点的总空间权重。
- :空间权重的平方和。
- :所有空间点的总数。
解释:
- 如果 值 大于 0,表示该基因的高表达区域在局部空间中聚集(正空间自相关)。
- 如果 值 小于 0,表示该基因在该区域的表达呈现离散模式(负空间自相关)。
EnSDD 采用 作为最近邻窗口大小,计算基因在每个空间点上的 统计量,并使用 Wilcoxon 检验 进一步确认哪些基因在特定空间域上表现出显著的空间可变性。
# 3. SA 在 EnSDD 中的应用
EnSDD 主要利用 Local Getis and Ord’s 统计量来:
- 筛选空间可变基因(SVGs):识别在不同空间域(Spatial Domain)中表达模式具有明显局部聚集或分散特征的基因。
- 分析组织结构中的基因表达模式:
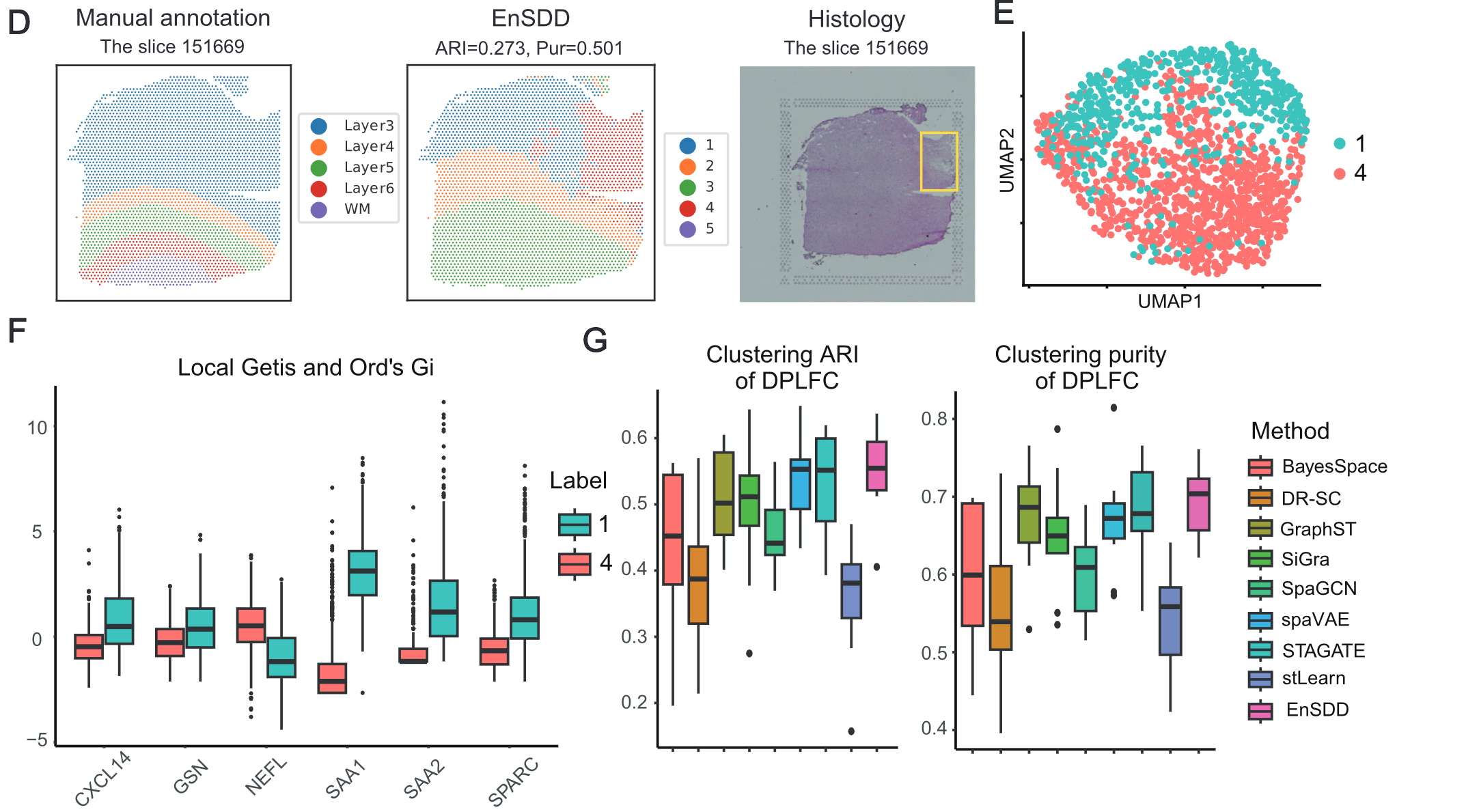
- 例如,在 人类 DLPFC(前额叶皮层)数据 中,EnSDD 发现 Layer 3 被进一步细分,并通过 统计量证实该区域内确实存在两个不同的基因表达聚集区域。
- 在 乳腺癌数据 中,利用 统计量找到了一些 与癌症进展相关的特异性基因(如 HEBP1、FAM234B、CSTA),它们在某些肿瘤区域内高度聚集。
# 4. 具体实现
# 步骤 1:计算局部空间自相关
对于每个基因:
- 构建 空间权重矩阵,选取最近的 6 个相邻点 作为参考。
- 计算 每个点的 统计量,得到基因的局部空间聚集度信息。
# 步骤 2:Wilcoxon 检验
对比不同空间域之间的基因表达水平,检验在某个空间域中是否存在显著表达变化的基因。
# 步骤 3:可视化和分析
- 局部空间自相关(SA)热图:展示不同基因在不同空间点上的 值,识别高表达聚集区域。
- 空间表达模式图:在组织切片上可视化基因的表达水平,观察其空间分布。
# 5. 实例解析
# 案例 1:人类前额叶皮层(DLPFC)
在 DLPFC 数据集中,EnSDD 发现:
- 在某些切片中,Layer 3 被自动分成两个子区域。
- 通过 统计量计算,发现 129 个基因在这两个子区域的表达显著不同。
- 进一步分析发现这些基因 与神经功能和甲状腺癌相关,揭示了 Layer 3 内部可能存在未被人工标注的异质性。
# 案例 2:乳腺癌肿瘤区域
- EnSDD 识别了 肿瘤中心区域(IDC_5) 和 周围免疫浸润区域,并通过 统计量找到了一组特异性基因:
- 在 IDC_5 高表达的基因:HEBP1(与乳腺癌进展相关)
- 在肿瘤边界高表达的基因:FAM234B(与肿瘤免疫浸润相关)
这些基因的空间表达模式揭示了 不同肿瘤区域的分子特征和潜在生物学机制,并可能成为新的肿瘤治疗靶点。
# 6. 总结
- 空间自相关(SA)是 EnSDD 识别空间可变基因(SVGs)的关键步骤。
- Local Getis and Ord’s 统计量用于衡量基因在局部空间的聚集或分散模式。
- 通过 SA 分析,EnSDD 发现了新的 组织异质性,并揭示了 肿瘤微环境 中的关键分子特征。
- 该方法在 人类大脑 DLPFC、小鼠大脑、乳腺癌、前列腺癌和卵巢癌 数据中均表现良好,能够有效提升空间转录组数据的生物学解释能力。
如果你对实现细节或代码感兴趣,可以让我帮你进一步解析如何在 Python 或 R 中实现 Local Getis and Ord’s 统计量计算!🚀
RCTD
# RCTD(Robust Cell Type Decomposition)
在 EnSDD 研究中,RCTD(Robust Cell Type Decomposition) 主要用于 推测空间转录组数据(SRT)中的细胞类型组成,即利用 单细胞转录组测序(scRNA-seq)数据 作为参考,对空间转录组数据中的每个 spot 进行 细胞类型分解(deconvolution)。
# 1. 什么是 RCTD?
RCTD 是一种 基于权重优化的去卷积方法,用于从空间转录组数据中估计每个 spot(空间点)中 不同细胞类型的组成比例。
在空间转录组数据(SRT)中,每个 spot 包含多个细胞的混合信号,而单细胞 RNA 测序(scRNA-seq)数据可以提供 单细胞级别的基因表达信息。RCTD 通过匹配 SRT 和 scRNA-seq 数据,估算每个 spot 内不同细胞类型的比例。
关键思想:
- 输入数据:
- 空间转录组数据(SRT):基因表达矩阵,每个 spot 可能包含多个细胞的混合基因表达。
- 单细胞 RNA-seq 数据(scRNA-seq):提供每种细胞类型的基因表达模式。
- 输出数据:
- 每个 spot 内部的 细胞类型组成比例,例如:
1
2Spot 1: 70% 肿瘤细胞, 20% 巨噬细胞, 10% 成纤维细胞
Spot 2: 50% 神经元, 30% 星形胶质细胞, 20% 少突胶质细胞
- 每个 spot 内部的 细胞类型组成比例,例如:
应用场景:
- 分析肿瘤微环境(TME),推测肿瘤区域内不同免疫细胞的分布情况。
- 探索大脑结构,研究不同皮层层次的细胞组成差异。
- 研究发育过程,分析不同组织区域的细胞类型变化。
# 2. RCTD 计算过程
# (1) 计算细胞类型的 “特征”
RCTD 通过 scRNA-seq 数据,获取每种细胞类型的特征基因表达模式。例如:
- 细胞类型 A:基因 1 高表达,基因 2 低表达。
- 细胞类型 B:基因 1 低表达,基因 2 高表达。
这些信息用于 构建细胞类型的特征矩阵。
# (2) 计算 SRT 数据中每个 spot 的基因表达模式
每个 spot 含有多个细胞,因此它的基因表达是 所有细胞类型的混合。RCTD 需要解出每个 spot 内 不同细胞类型的贡献比例。
# (3) 通过权重优化分解细胞类型
RCTD 假设 SRT 中每个 spot 的基因表达 由 不同细胞类型的加权平均表达 组成:
\begin{align} X = W \cdot C + \epsilon \end{align}其中:
- 是 SRT 数据的基因表达矩阵(待解)。
- 是 scRNA-seq 参考数据中每种细胞类型的基因表达模式(已知)。
- 是权重矩阵(待求解),表示每种细胞类型在每个 spot 的贡献比例。
- 是噪声项。
RCTD 采用 贝叶斯方法 + 线性优化 来求解 ,从而估计每个 spot 内部的细胞类型组成。
# (4) 归一化 & 计算细胞类型分布
为了确保所有细胞类型的比例总和为 1,RCTD 进行归一化处理,最终输出每个 spot 的细胞组成。
# 3. RCTD 在 EnSDD 研究中的应用
EnSDD 通过 RCTD 进行细胞类型推测,帮助分析 不同空间域的细胞组成,特别是在 肿瘤微环境分析 方面表现突出。例如:
# (1) 在乳腺癌数据中的应用
- 目标:分析肿瘤中心(IDC_5)与肿瘤边缘的细胞类型组成差异。
- 结果:
- IDC_5 肿瘤中心:癌细胞比例高,免疫细胞(如巨噬细胞、树突状细胞)比例低。
- 肿瘤边缘区域:免疫细胞(如巨噬细胞和树突状细胞)显著富集,可能与 肿瘤免疫逃逸机制 相关。
细胞比例结果(示例):
| Spot | 癌细胞 | 巨噬细胞 | 树突状细胞 | CD4+ T 细胞 |
|---|---|---|---|---|
| 1 | 70% | 10% | 10% | 10% |
| 2 | 40% | 30% | 20% | 10% |
# (2) 在前列腺癌数据中的应用
- 目标:研究肿瘤区域(Tumor)和肿瘤边界(Ecotone)的细胞类型差异。
- 结果:
- 肿瘤区域:以 LE-KLK3 阳性上皮细胞 为主。
- 肿瘤边界(Ecotone):更高比例的 免疫细胞(MNP 和 B 细胞),可能影响肿瘤的进展和免疫治疗反应。
# (3) 在卵巢癌数据中的应用
- 目标:分析肿瘤、肿瘤 - 基质交界(Ecotone)和基质区域的细胞组成。
- 结果:
- 肿瘤区域:EOC(上皮性卵巢癌细胞)占比高。
- 肿瘤 - 基质交界:富含 上皮细胞、成纤维细胞(CAFs)、间皮细胞,可能在肿瘤侵袭过程中发挥作用。
# 4. RCTD 与其他方法的对比
| 方法 | 原理 | 适用数据 | 主要特点 |
|---|---|---|---|
| RCTD | 基于权重优化的细胞去卷积 | scRNA-seq + SRT | 计算准确,适用于高噪声数据 |
| Seurat (SPOTlight) | 线性回归 + NMF | scRNA-seq + SRT | 适用于简单组织 |
| Stereoscope | 贝叶斯概率模型 | scRNA-seq + SRT | 适用于大规模数据 |
| Cell2location | 空间层次贝叶斯模型 | scRNA-seq + SRT | 适用于大规模数据,推测稀有细胞类型 |
相比 Seurat 和 Stereoscope,RCTD 对噪声的鲁棒性更强,适用于高复杂度的组织,如癌症组织和大脑皮层。
# 5. 结论
- RCTD 用于估计 SRT 数据中每个 spot 的细胞组成,帮助 EnSDD 解析不同空间域的细胞类型分布。
- 通过 scRNA-seq 参考数据,RCTD 能够揭示 肿瘤微环境、神经组织层次结构等。
- 在 乳腺癌、前列腺癌、卵巢癌 数据中,RCTD 发现了 肿瘤 - 免疫相互作用的关键特征,有助于癌症生物标志物发现和治疗策略优化。
RCTD
# Purity(Pur,纯度)
Purity(纯度) 是一个用于评估聚类(Clustering)质量的指标,衡量聚类结果与真实类别标签(Ground Truth)的一致性。它的取值范围为 $$\begin{align}0, 1\end{align}$$,值越高,表示聚类结果越接近真实分类。
# 1. Purity 公式
\begin{align} \text{Purity} = \frac{1}{N} \sum_{l=1}^{L} \max_{t} |u_l \cap v_t| \end{align}其中:
- :样本总数(数据点总数)。
- :预测聚类的数量(即 EnSDD 识别出的空间域数)。
- :真实类别(Ground Truth)数量(如人工标注的组织结构)。
- :第 个预测聚类(即 EnSDD 识别出的某个空间域)。
- :第 个真实类别(如已知组织切片的层级)。
- :预测聚类 内属于真实类别 的样本数量。
- :对于每个预测的聚类 ,找出其中最多的真实类别样本数量。
解释:
- 对于每个预测的聚类 ,找出其中占比最多的真实类别 。
- 求所有预测聚类的占比最多真实类别样本数的总和,并除以总样本数 ,得到纯度值。
# 2. Purity 计算示例
# (1) 示例数据
假设我们有 10 个数据点,它们的真实类别(Ground Truth)和聚类算法(如 EnSDD)给出的预测聚类如下:
| 数据点编号 | 真实类别 (Ground Truth) | 预测聚类 (Clustering) |
|---|---|---|
| 1 | A | 1 |
| 2 | A | 1 |
| 3 | A | 2 |
| 4 | B | 2 |
| 5 | B | 2 |
| 6 | B | 3 |
| 7 | C | 3 |
| 8 | C | 3 |
| 9 | C | 3 |
| 10 | C | 3 |
# (2) 计算每个聚类的最大类别
聚类 1(u₁):
- 真实类别 A:2 个
- 最大类别:A(2)
聚类 2(u₂):
- 真实类别 A:1 个
- 真实类别 B:2 个
- 最大类别:B(2)
聚类 3(u₃):
- 真实类别 B:1 个
- 真实类别 C:4 个
- 最大类别:C(4)
# (3) 计算 Purity
\begin{align} \text{Purity} = \frac{2 + 2 + 4}{10} = \frac{8}{10} = 0.8 \end{align}# 3. Purity 在 EnSDD 论文中的应用
在 EnSDD 研究中,Purity 主要用于 评估空间域划分(Spatial Domain Detection)的准确性,即检查 EnSDD 生成的空间域与人工标注的组织结构(如大脑层次结构或肿瘤组织分区)的匹配程度。
# 实验结果示例
- 在 人类大脑 DLPFC 数据集 中:
- EnSDD 纯度(Purity)= 0.704,优于 STAGATE(0.678)和 spaVAE(0.672)。
- 在 乳腺癌数据 中:
- EnSDD 纯度(Purity)= 0.668,高于其他方法。
这些结果表明,EnSDD 生成的空间域划分与真实组织结构的匹配度较高,能够更好地识别不同的组织区域。
# 4. Purity 与 Adjusted Rand Index(ARI)的区别
| 指标 | 适用情况 | 计算方法 | 取值范围 | 主要特点 |
|---|---|---|---|---|
| Purity(纯度) | 评估聚类质量 | 计算每个预测聚类中最大类别样本数的比例 | [0,1] | 直观易懂,但不能惩罚错误分类 |
| ARI(调整兰德指数) | 评估聚类与真实类别的一致性 | 计算正确分类与随机分类的差值 | [-1,1] | 适用于类数量不均衡的数据,惩罚错误分类 |
总结:
- Purity 直观易懂,适合快速评估聚类质量,但它 不考虑错误分类的影响,如果一个大类被错误拆分成多个小类,Purity 仍然可能较高。
- ARI 更加严格,它不仅考虑正确分类,还会对错误分类进行惩罚,因此对于聚类方法的评估更为精确。
在 EnSDD 论文中,Purity 和 ARI 一起使用,以确保空间域检测方法的可靠性。
# 5. 结论
- Purity 衡量聚类质量,数值越高,说明 EnSDD 预测的空间域更接近真实组织结构。
- 与 ARI 结合使用时,Purity 提供直观的匹配度衡量,而 ARI 可检测错误分类的影响。
- 在 EnSDD 研究中,Purity 证明了该方法比 STAGATE、spaVAE 等方法具有更好的空间域检测能力。
如果你想了解 代码如何计算 Purity 或者 如何优化空间域划分算法,可以告诉我,我可以进一步解析!
# 总结
在 Methods 部分,论文的关键在于如何将来自不同方法的聚类结果转化为二值相似矩阵,并利用上述优化模型进行加权融合,生成一个能够反映综合信息的共识相似矩阵。通过引入负熵正则化项,模型在防止过拟合的同时,也为各基础方法赋予了合理的权重。最终,这一共识相似矩阵被用来指导 Louvain 算法实现空间域的自动划分,进而为后续的基因表达和细胞类型分布分析提供基础。
# 代码
由于代码是 R 语言书写的,不熟悉的地方很多,特此全面的记录解读一番。
# run_individual_clustering
1 | apply_BayesSpace <- function(Seurat.data, platform = "Visium", n.PCs = 15, n.HVGs = 2000, |
BayesSpace
当然可以,我们来逐行解读这个 apply_BayesSpace 函数。它的功能是:在一个 Seurat 对象上使用 BayesSpace 包进行空间转录组聚类分析。你这段代码流程很完整,也有些细节挺有意思,我会分块讲解,穿插解释函数作用和每一步背后的意图。
# 🧠 函数定义和参数说明:
1 | apply_BayesSpace <- function(Seurat.data, platform = "Visium", n.PCs = 15, n.HVGs = 2000, |
Seurat.data:传入一个处理过的 Seurat 对象,假设已经做完 SCTransform。platform:平台类型,如"Visium"或"ST"(决定空间结构等处理方式)。n.PCs:PCA 主成分数量,默认为 15。n.HVGs:选择前多少个高变基因(Highly Variable Genes)。n.setting:聚类数量,即q值,默认是 7 类。nrep:MCMC 采样的迭代次数,BayesSpace 聚类时使用,默认 50000。
# 📦 步骤一:从 Seurat 对象中提取数据
1 | exp_data <- list(counts = as.matrix(Seurat.data@assays$SCT@counts), |
- 提取标准化前后的表达矩阵:
counts: 原始计数logcounts: SCT 标准化后的 log-scale 表达值
1 | df <- Seurat.data@meta.data[, c("x", "y", "pixel_x", "pixel_y")] |
- 从元数据中提取空间坐标。
1 | temp_colnames <- colnames(df) |
BayesSpace需要用row,col命名空间位置,所以这里做了列名替换。
# 📦 步骤二:构造 SingleCellExperiment 对象
1 | sce <- SingleCellExperiment::SingleCellExperiment(assay = exp_data, colData = df) |
- 创建一个符合 Bioconductor 标准的数据容器,包含表达矩阵和元数据。
BayesSpace是以SingleCellExperiment为输入格式。
# 📈 步骤三:寻找高变基因并 PCA
1 | dec <- scran::modelGeneVar(sce) |
- 用
scran估计每个基因的变异程度,选择前n.HVGs个变异最大的基因(通常对降维和聚类效果好)。
1 | set.seed(102) |
- 在 top HVGs 上做 PCA 降维。
# 🧼 步骤四:预处理空间信息
1 | sce <- BayesSpace::spatialPreprocess(sce, platform=platform, skip.PCA=TRUE) |
- 执行
BayesSpace所需的空间预处理:skip.PCA=TRUE表示我们已经做过 PCA,不重复。- 添加空间网格、邻接矩阵等结构信息。
# 🎚️ 步骤五:设置 gamma 超参数(平台特异)
1 | if(platform == "Visium"){ |
gamma是 BayesSpace 聚类模型的平滑参数,控制聚类边界的 “平滑程度”。
# 🔁 步骤六:执行 BayesSpace 聚类
1 | set.seed(150) |
- 开始空间聚类:
q: 聚类的簇数d: 使用的 PCA 数量(如前 15 个)nrep: MCMC 迭代次数(越多越稳定但越慢)
# 📊 步骤七:提取聚类结果
1 | res.cluster <- sce$spatial.cluster |
- 聚类结果是一个向量(每个 spot 的聚类标签)。
- 给结果加上对应 spot 的名字。
# 🔁(注释掉的代码)自动寻找最佳聚类数
1 | # sce <- BayesSpace::qTune(...) |
- 这段注释代码原本用于自动寻找最优
q值(聚类数),通过比较对数似然。但作者这里选择手动设定n.setting。
# 🔚 返回结果
1 | return(res.cluster) |
- 返回一个聚类结果向量,用户可以根据它进行可视化、下游分析等。
# ✅ 总结一句话:
这个函数将 Seurat 对象转换为
SingleCellExperiment,挑选高变基因做 PCA,然后用BayesSpace进行空间聚类分析,并返回每个 spot 的聚类标签。
你可以配合 BayesSpace::clusterPlot(sce) 进行可视化,也可以把这个结果加到 Seurat 对象里,继续做差异分析。
如果你还想了解聚类原理或者对某个包函数不理解,可以继续问我!
1 | apply_SpaGCN <- function(Seurat.data, SpaGCN_beta = 55, SpaGCN_alpha = 1, SpaGCN_p = 0.5, |
SpaGCN
当然可以!下面我来逐行解读这段 apply_SpaGCN 函数的 R 代码。这段代码的功能是:调用 Python 实现的 SpaGCN 空间聚类算法,并返回聚类结果。它通过 reticulate 接口从 R 中运行 Python 脚本。
# 🧠 函数定义及参数说明
1 | apply_SpaGCN <- function(Seurat.data, |
Seurat.data: Seurat 对象(空间数据),包含图像路径信息SpaGCN_beta,SpaGCN_alpha,SpaGCN_p,SpaGCN_l: 是 SpaGCN 聚类算法的超参数,控制空间权重、邻域强度等num.cluster: 聚类簇数量res.setting: 聚类分辨率设置(用户自定义)SpaGCN_lr: 学习率SpaGCN_epoches: 训练迭代次数platform: 平台,如 "Visium",决定空间坐标解读方式
# 📦 1. 提取图像路径
1 | temp <- Seurat.data@images |
假设 Seurat.data@images 存放了一些自定义字段(比如用 $counts_path 来表示 count 矩阵路径、meta 信息和图像路径):
counts_path: 表达矩阵(spot × gene)的文本路径meta_path: spot 的空间位置信息img_path: H&E 图像文件路径
⚠️ 这些字段可能是你自己前期写入 SeuratObject@images 的,不是默认字段。
# 🐍 2. 加载 Python 脚本
1 | reticulate::source_python(system.file("python", "apply_spaGCN.py", package = "EnSDD")) |
source_python(...):通过 R 的reticulate包加载 Python 脚本system.file(...):定位 R 包EnSDD中的apply_spaGCN.py脚本路径- 假设你安装了一个 R 包叫
EnSDD,它里面封装了运行 SpaGCN 所需的 Python 脚本
- 假设你安装了一个 R 包叫
📝 被注释的 EnSDD_pyexec(...) 也可能是某个自定义封装,但你实际使用的是 reticulate 。
# 🚀 3. 调用 Python 的 run_spaGCN 函数
1 | run_spaGCN(counts_path, meta_path, img_path, |
- 这个函数在
apply_spaGCN.py中定义,接收参数并执行 SpaGCN 空间聚类任务 - SpaGCN 是一个 GCN(图卷积网络)框架,结合空间坐标和图像信息进行聚类
- 参数解析:
b = beta:控制空间光滑性a = alpha、p:控制边权的计算n_clusters:聚类个数res_setting_by_user: 分辨率lr: 学习率max_epochs: 迭代次数
✅ 此处训练过程全在 Python 中执行,输出为文件结果。
# 📁 4. 加载结果并处理
1 | res.path <- paste0(dirname(img_path), "/spaGCN_res", "/spaGCN_label.txt") |
- Python 会在图片所在文件夹下创建
spaGCN_res/spaGCN_label.txt - 文件中记录的是:
spot名称 \t 聚类标签 - 把
V2作为聚类标签,V1为 spot 名,转换为一个 R 命名向量
# 🔢 5. SpaGCN 聚类结果中可能含有 "0" 类 → 调整为从 1 开始
1 | if(sum(res == 0) != 0){ |
- 如果存在 0 类,就全部 +1,使得聚类编号从 1 开始(防止误差)
# ✅ 6. 根据 Seurat 的列顺序排列聚类结果,并清理中间文件夹
1 | res <- res[colnames(Seurat.data)] |
- 确保返回的聚类向量顺序和 Seurat 中列顺序一致
- 删除 SpaGCN 临时输出文件夹,避免污染
- 返回:spot-level 聚类标签
# 🎉 总结一句话:
apply_SpaGCN()是一个 R 函数,用于封装和调用 Python 的SpaGCN空间聚类过程,输入是 Seurat 对象,输出是每个 spot 的聚类标签。
如果你想看 apply_spaGCN.py 文件里 run_spaGCN() 是如何实现的,也可以把那个 Python 文件贴给我,我可以继续帮你逐行解读~
或者你想把这个结果接回 Seurat 进行可视化的话,也可以问我哦。
1 |
|
run_individual_clustering
当然可以!这段代码是一个 STAGATE 方法的调用和结果处理模块,通常嵌套在一个更大的函数体内,负责:
运行 STAGATE 空间聚类,记录运行时间,处理聚类结果并保存。
我会按逻辑结构详细解释每个部分👇:
# ✅ 1. 判断是否执行 STAGATE 聚类
1 | if(STAGATE){ |
- 如果传入的
STAGATE参数为TRUE,就会执行 STAGATE 聚类分析。
# 🧪 2. 调用 apply_STAGATE() 函数并计时
1 | cat("Run STAGATE...\n") |
- 打印提示语:
Run STAGATE... - 记录开始时间
pred.STAGATE - 调用 STAGATE 聚类函数
apply_STAGATE(),传入参数:Seurat.data:Seurat 格式空间转录组对象number.setting.by.user:用户设定的聚类簇数STAGATE_alpha:控制聚类图平滑程度的参数(STAGATE 超参数)
- 记录结束时间
end.STAGATE - 计算运行时间(分钟)
time.STAGATE
# 📝 3. 保存 STAGATE 聚类结果到列表对象中
1 | cat("Run time for STAGATE: ", time.STAGATE, "min","\n") |
- 输出 STAGATE 的运行时间
- 把运行时间加入时间列表
time.methods - 把聚类标签结果
temp.STAGATE保存进聚类结果列表res.clustering$STAGATE k是用来统计或记录方法数量的变量,这里自增(可能用于 ensemble 阶段)
# 🧼 4. 检查是否有包含 NA 的聚类方法,清理无效结果
1 | names(time.methods) <- Methods.used |
- 将时间向量命名(与方法对应)
- 检查每种聚类方法的结果中是否存在 NA 值
- 如果某方法含 NA,就将其索引加入
index.list
# 🧽 5. 删除含 NA 的聚类方法
1 | if(length(index.list) != 0){ |
- 若有 NA,获取含 NA 方法的名称
- 从结果列表中将其移除(设置为 NULL)
# 📐 6. 聚类向量转为矩阵(后续可用于 ensemble)
1 | res.clustering.matrix <- lapply(res.clustering, clust2Mat) |
clust2Mat:将每种方法的聚类标签向量转换为 二值指示矩阵(每行一个样本,每列一个簇,1 表示属于某簇)
# 📦 7. 打包最终结果为列表对象
1 | res <- list( |
结构说明:
clustering.vec: 不同方法对应的聚类标签向量(含 STAGATE)clustering.mat: 聚类标签的二值表示矩阵(用于后续集成)time: 每种方法的运行时间
# 💾 8. 可选保存结果到 .RData
1 | if(saving_results) |
- 如果
saving_results = TRUE,则保存结果到res.clustering.RData文件
# 🔚 9. 返回最终聚类结果对象
1 | return(res) |
# 🔁 总结一下这段代码做了什么?
| 步骤 | 操作 |
|---|---|
| 1 | 判断是否启用 STAGATE 方法 |
| 2 | 调用 apply_STAGATE() 聚类,记录时间 |
| 3 | 将结果保存到列表,统计运行时间 |
| 4 | 清除含 NA 的聚类方法结果 |
| 5 | 转换聚类结果为二值矩阵 |
| 6 | 打包为列表,保存到本地 |
| 7 | 返回聚类结果 |
如果你还想看看 apply_STAGATE() 的具体内容(即 STAGATE 是如何被调用、处理数据的),可以发我代码,我也可以逐行讲解!
或者你也可以告诉我,你是在哪个项目 / 代码库里看到的这些,比如是 EnSDD、SpaGCN 或其他空间分析工具~我可以更有针对性地解释模块设计逻辑。
clust2Mat
clust2Mat: Function to compute adjacency matrix of cluster graph given a vector of cluster memberships
Description
Given a list of cluster memberships, this function computes the adjacency matrix for the associated cluster graph. The adjacency matrix is a matrix whose rows and columns are the nodes of the cluster graph and whose entries are 0's or 1's. A 1 entry indicates that the corresponding nodes are connected, and a 0 indocates that they are not.
Usage
clust2Mat(memb)
Arguments
memb
A numeric vector, with each entry representing a node, the entry's value being the number of the cluster to which that node belongs.
Value
Details
Given a vector of cluster membership numbers, where the number of entries is the number of nodes n, the function computes an nxn ``adjacency matrix'' for the corresponding cluster graph. The cluster graph is the graph in which two nodes are connected by an edge if and only if they are members of the same cluster. The adjacency matrix for the graph has rows and columns representing the nodes, in the same order as the input vector. The (i,j) entry is 1 if and only if node i and node j are in the same cluster. Otherwise, the entry is 0. By convention, diagonal entries are 0.
# Spatial domain detection
1 | ## setting the number of clustering equal to the annotation provided by SEDR |
Spatial doamin detection
当然可以!我们一起来逐行解读这段代码,它的作用是:
基于多个聚类数量设置运行聚类分析,并可视化每种聚类结果(例如用于 EnSDD 的聚类 ensemble 处理)。
它主要涉及:
- 加载 Python 脚本(可视化)
- 读取多个不同聚类数下的聚类结果
- 做 ensemble 聚类(融合多个方法 / 模型结果)
- 用 Louvain 算法在相似度矩阵上聚类
- 存储结果并生成聚类可视化图像
# 🔧 准备阶段
1 | ## setting the number of clustering equal to the annotation provided by SEDR |
reticulate: 用于 R 调用 Pythonsource_python(...): 加载 Python 文件(用于空间聚类可视化visualization_clustering())
1 | label_setting <- c(10, 16, 17, 20, 25) |
label_setting: 聚类数的多个设置(不同聚类簇个数)sankey_df: 用来保存每个设定下的聚类标签,可能用于后续的 Sankey plot 可视化流向图
# 🔁 遍历多个聚类数设定
1 | for (i in 1:length(label_setting)) { |
逐个设置聚类簇数,准备执行后续流程。
# 📦 加载已有的聚类结果 .RData
1 | res.tmp <- load(paste0("../data/res_individual_", label_setting[i], "_all.RData")) |
- 加载保存好的结果文件
- 结果中保存了
clustering.mat(聚类标签矩阵)和clustering.vec(单一聚类标签向量)
# 🧠 聚类结果融合(Ensemble)
1 | res.ensemble <- solve_ensemble(res$clustering.mat, lambda = NULL, prob.quantile = 0.5, niter = 100, epsilon = 1e-5) |
使用 solve_ensemble() 函数对聚类矩阵做 集成聚类融合:
clustering.mat: 多模型、多参数下的聚类标签(行:spot,列:不同聚类方案)- 输出
res.ensemble$H: 相似度矩阵(用于后续 Louvain 聚类)
# 📊 Louvain 聚类(基于集成的相似度网络)
1 | sim_net_louvain <- res.ensemble$H |
- 使用
Louvain_clustering_binary()对相似度矩阵H进行社区检测(聚类) setting_k: 目标聚类数max.res: 最大分辨率(控制 Louvain 聚类是否更细或更粗)
# 📝 聚类结果格式化并保存
1 | meta_data <- Seurat.data@meta.data |
- 构造一个包含两个聚类标签的 data frame:
- 原始标签:
res.vec - 融合聚类标签(EnSDD 集成结果):
res.ensemble.clustering.louvain
- 原始标签:
# 🗂 结果写入文件并加入总表
1 | domain_name <- paste0('Domain_', label_setting[i]) |
- 把每个聚类设定的集成标签加入
sankey_df,方便后续绘制 Sankey 流图 - 将聚类结果保存为
.txt文件,以便后续可视化或分析
# 🖼 调用 Python 进行聚类可视化
1 | meta_data_path <- paste0("../data/clustering.res.", label_setting[i], ".txt") |
使用之前加载的 Visualization_HBC_clustering.py 中的 visualization_clustering() :
- 输入:
- 表达数据(
counts_path) - 聚类结果路径
- 图像路径
- 表达数据(
- 输出:空间聚类的图像(spot 被聚类标签着色)
# 🧹 清理(注释掉)
1 | # unlike('res.clustering.txt') |
这行可能是个笔误或作者写错了,可能本意是 unlink() 删除文件。
# ✅ 总结一句话:
该代码是为了测试多个聚类簇数设置下的空间聚类效果,结合 EnSDD 的聚类融合方法和 Python 的可视化函数,输出空间聚类图和标签,为后续分析(如 Sankey plot)做准备。
如果你有任何一个函数想继续详细分析(比如 solve_ensemble() 或 visualization_clustering() 的内部逻辑),可以发我,我继续给你拆解!😎
# solve_ensemble 关键
1 |
|
solve_ensemble
好呀!我们来详细解读一下这个 solve_ensemble 函数 —— 它实现的是一个聚类集成(Ensemble Clustering)方法,用于融合多个聚类结果,输出一个共识相似度矩阵 H ,并自动学习每个聚类结果的权重 w 。
# 🧠 目标简述
1 | solve_ensemble(Results.clustering, ...) |
- 输入:多个聚类方法生成的样本 - 样本相似度矩阵(比如你前面问过的
clust2Mat转换出来的) - 输出:
H:最终融合后的相似度矩阵(作为新的聚类输入)w:每个方法的权重(表示该方法对最终共识的贡献程度)
该方法基于一个优化目标,使用迭代优化来寻找最合适的加权平均。
# 📥 输入参数说明
| 参数 | 含义 |
|---|---|
Results.clustering | list 类型,多个方法生成的相似度矩阵,每个元素是一个 N×N 矩阵 |
lambda | 平衡主损失项和熵正则项的超参数,如果为空,会根据分布自适应选择 |
prob.quantile | 用于估计 lambda 的分位数(默认 0.5,代表中位数) |
niter | 最多迭代次数 |
epsilon | 收敛判据:两次迭代的总损失变化小于这个值时停止 |
# 🔧 算法结构详解
# 1. 参数初始化
1 | num.methods <- length(Results.clustering) |
拿到方法数量、样本数、细胞类型数(实际没用)。
# 2. 初始化权重和共识矩阵
1 | w <- rep(1 / num.methods, num.methods) # 初始权重平均 |
📌 共识矩阵 H 是多个相似度矩阵的加权平均。
# 3. 计算初始 loss 和 lambda(如未指定)
1 | temp2 <- sapply(Results.clustering, L2_norm, Y = H) |
temp2是每个方法和当前共识矩阵之间的 L2 距离(差异)。- 如果没有指定
lambda,就根据这些距离的分布自适应选一个中位数。
# 4. 主循环:迭代优化权重和共识矩阵
1 | while (k <= niter) { |
每一轮迭代包括 3 步:
# 🌀 步骤 1:更新权重
1 | temp2 <- sapply(Results.clustering, L2_norm, Y = H) |
- 越接近
H的聚类方法,其权重w越大。 - 形式上是 Softmax,受
lambda控制平滑程度。
# 🌀 步骤 2:更新共识矩阵
1 | H <- Reduce("+", Map("*", Results.clustering, w)) |
- 用新的权重对所有相似度矩阵加权平均。
# 🌀 步骤 3:计算损失函数
1 | loss_main <- sum(sapply(Results.clustering, L2_norm, Y = H) * w) |
- 主损失
loss_main:共识矩阵和原始方法之间的加权差异 - 正则项
loss_entropy:鼓励权重分布均匀,避免过拟合 - 总损失是两者的加权和
# 5. 收敛判断与跳出循环
1 | diff_iter <- abs(loss_all - loss_all_temp) |
# 6. 返回结果
1 | return(list(H = H, w = w)) |
# ✅ 最终输出解释
1 | list( |
你可以把 H 当作一个新的样本之间的相似度矩阵,再送入例如 Louvain 聚类、谱聚类等进一步聚类分析中。
# 📌 总结一张图(逻辑结构)
1 | 多种聚类结果(A, B, C...) => [相似度矩阵1, 2, 3...] |
如果你也想看 L2_norm 这个函数我也可以帮你查或分析下~
# utils
# data_process
1 | data_process <- function(counts_path, loc_path, img_path, n_HVG = 2000, n_PCA = 20){ |
dataprocess
这段 R 代码定义了一个用于空间转录组数据预处理的函数 data_process 。它使用了 Seurat 包来创建 Seurat 对象并执行标准的数据预处理流程(如标准化、变量基因筛选、PCA)。下面是对这段代码逐行的详细解析:
# 🔧 函数定义
1 | data_process <- function(counts_path, loc_path, img_path, n_HVG = 2000, n_PCA = 20) |
定义了一个函数 data_process ,接受以下参数:
counts_path:表达矩阵的路径(行是基因,列是空间点)loc_path:空间位置信息的路径(spot 坐标)img_path:图片路径,暂时没被实际读取n_HVG:选择多少个高变异基因(默认 2000)n_PCA:使用多少主成分进行 PCA(默认 20)
# 📂 读取表达矩阵
1 | counts = read.table(counts_path, sep = '\t') |
读取表达矩阵文件,并转为矩阵形式。假设行为基因、列为空间点(spot)。
# 📍 读取坐标信息
1 | coordinates <- data.frame(read.table(loc_path, sep = '\t')) |
读取空间坐标信息,通常包含每个 spot 的 x , y 坐标。
# 🧬 对齐 counts 和坐标
1 | colnames(counts_ST) <- rownames(coordinates) |
将 counts_ST 的列名设置为空间坐标的 rownames,确保表达矩阵的列与坐标信息对齐。
# 🔬 创建 Seurat 对象
1 | suppressWarnings({ |
用表达矩阵和空间坐标创建一个 Seurat 对象,使用 Spatial 作为 assay 名称,并把坐标作为元数据添加进去。
# 📊 标准化处理
1 | Seurat.ST <- Seurat::SCTransform(Seurat.ST, assay = "Spatial", verbose = FALSE) |
使用 SCTransform 对数据进行标准化,这是一种较新的标准化方法,比传统的 NormalizeData 更鲁棒。
# 📈 高变异基因选择
1 | Seurat.ST <- Seurat::FindVariableFeatures(Seurat.ST, nfeatures = n_HVG, verbose = FALSE) |
从标准化后的数据中选择 n_HVG 个高变异基因(默认 2000 个)。
# 📐 PCA 降维
1 | Seurat.ST <- Seurat::ScaleData(Seurat.ST, verbose = FALSE) |
先对数据标准化(center & scale),再进行 PCA 降维,保留 n_PCA 个主成分。
# 🖼️ 处理图片信息(未使用)
1 | data.list <- list(counts_path = counts_path, loc_path = loc_path, img_path = img_path) |
将文件路径信息存储到 Seurat.ST@images 槽中。注意这里并没有真正读入图像,只是把路径作为一个列表存进去。如果后续不使用这个结构,可能没太大意义。
# 🔁 返回结果
1 | return(Seurat.ST) |
返回预处理后的 Seurat 对象。
# ✅ 总结
这是一个用于空间转录组数据预处理的函数,完成了以下几步:
- 读取表达矩阵与坐标
- 创建 Seurat 对象
- SCTransform 标准化
- 选择高变异基因
- PCA 降维
- 保存原始路径信息到 Seurat 对象中
如你后续要加上图像处理功能(例如和 histology 图像配准),可以使用 Read10X_Image() 或 ReadImage() 之类的方法来真正地载入图像。
如果你有具体的输入数据结构(比如坐标文件长什么样),我也可以帮你判断这段代码是否能跑通,或者怎么修改以适应不同的数据来源。你想继续深入看看这部分吗?
# clust2Mat
1 | clust2Mat <- function(memb){ |
clust2Mat
这段 R 代码定义了一个名为 clust2Mat 的函数,用于把聚类标签(cluster membership)向量转换成一个 共聚类关系矩阵。下面我们来逐步分析:
# 🔧 函数定义
1 | clust2Mat <- function(memb){ |
memb是一个向量,表示每个样本的聚类标签。- 可以是一个具名向量(比如
names(memb)是样本名)。 - 每个元素的值是对应样本所属的聚类编号。
- 可以是一个具名向量(比如
# 📏 获取样本数量
1 | N <- length(memb) |
- 获取一共多少个样本(即多少个聚类成员)。
# 📐 构造共聚类矩阵
1 | mat_cn <- as.numeric(outer(memb, memb, FUN = "==")) - outer(1:N, 1:N, "==") |
这是核心逻辑。逐步拆解如下:
# ✅ outer(memb, memb, FUN = "==")
- 构造一个
N x N的矩阵,表示每对样本是否属于同一个聚类。 - 例如,如果
memb = c("A" = 1, "B" = 1, "C" = 2),则结果是:
1 | A B C |
# ✅ as.numeric(...)
- 把逻辑值
TRUE/FALSE转为1/0。
# ✅ outer(1:N, 1:N, "==")
- 构造一个对角矩阵,主对角线上是
TRUE,其他是FALSE,表示i == j,也就是样本与自身是否相等。
# ✅ 两者相减:
1 | as.numeric(outer(memb, memb, FUN = "==")) - outer(1:N, 1:N, "==") |
这样可以将对角线上的 “自我比较” 从 1 减为 0 ,避免误判为共聚类(因为我们通常不关心 “自己和自己” 是否在一类中)。
# ✅ 举个例子:
如果:
1 | memb <- c("A" = 1, "B" = 1, "C" = 2) |
则:
1 | outer(memb, memb, "==") = |
减去对角线:
1 | A B C |
说明:
A和B属于同一类,设为 1- 自己和自己不算,设为 0
C和其他不同类,设为 0
# 🏷️ 设置行列名
1 | rownames(mat_cn) <- names(memb) |
给矩阵的行列设置名字,以方便后续查看或可视化。
# 🔁 返回矩阵
1 | return(mat_cn) |
返回共聚类矩阵。
# ✅ 总结
这个函数的作用是:
将聚类结果向量
memb转换为一个 共聚类矩阵,其中:
- 如果两个样本属于同一个聚类,值为
1- 否则为
0- 对角线(自己和自己)是
0
# 👀 应用场景
这种矩阵常用于:
- 聚类结果的可视化(热图)
- 多个聚类之间的一致性比较(比如聚类稳定性评估)
- 作为图结构的邻接矩阵输入
如果你打算用这个矩阵进一步构建图、聚类评价指标(比如 NMI、ARI)或者做图神经网络的输入,也可以继续聊,我可以帮你转换或对接成你要的格式!
# solve_ensemble
1 | ########### ensemble strategy ############### |
solve_ensemble
你贴的这段 R 代码 solve_ensemble 实现了一个 自适应加权集成聚类算法,用于将多个二值相似度矩阵(通常是从不同算法得到的聚类结果)合并为一个集成结果,关键是:自动学习每个方法的权重。
我给你拆解成几个直观的模块来讲:
# 🧩 1. 函数目标概述
这个函数的目标是:
根据多个聚类 / 相似性矩阵,学习出一个最佳的加权平均矩阵(
H),并同时学习出每个矩阵的权重(w)。
# ⚙️ 2. 输入参数说明
1 | solve_ensemble <- function(Results.clustering, lambda = NULL, prob.quantile = 0.5, |
Results.clustering:一个 list,包含多个 spot × spot 的二值相似度矩阵(比如是否同属一类)。lambda:控制权重平滑程度的超参数。若为NULL,则自动估计(后面会说怎么估)。prob.quantile:如果lambda = NULL,就用这参数来通过多个方法间差异的分布估计 lambda。niter:最大迭代轮数。epsilon:损失函数收敛的阈值,若变化小于此值就停止。
# 🔁 3. 核心迭代部分解析
# ✅ 初始化
1 | w <- c(rep(1/num.methods, num.methods)) |
- 初始时:给每个相似度矩阵一个平均权重
1/num.methods - 用
Reduce + Map加权平均得到初始集成相似矩阵H
# 🔄 迭代更新
每轮做两件事:
# ① 更新每个相似度矩阵的 “离散度”
1 | temp2 <- sapply(Results.clustering, L2_norm, Y = H) |
这个 temp2 是每个矩阵与当前集成矩阵 H 的 L2 距离,越小表示越接近集成矩阵,说明该方法越 “可靠”。
L2_norm(A, Y)是外部定义的函数,表示矩阵 Frobenius 距离:
# ② 自动设置 lambda(如果第一次设置为 NULL)
1 | if(is.null(lambda)){ |
lambda 控制每个方法的重要程度是否能显著拉开;比如选第 50% 分位作为自动估计值。
# ✅ 更新权重 w
1 | w <- exp(-temp2/lambda)/sum(exp(-temp2/lambda)) |
这一步是关键:根据每个方法和 H 的距离,做一个 softmax,加权越小的越重要(因为它离 H 更近)。
类似于加权平均的 soft attention 机制。
# ✅ 重新计算 H
1 | H <- Reduce("+", Map("*", Results.clustering, w)) |
用新的权重更新集成矩阵。
# ✅ 计算损失函数
1 | loss_main <- sum(sapply(...)) |
总损失由两部分组成:
- 主要误差项(
loss_main):每个矩阵和集成矩阵的距离(代表一致性) - 熵正则项(
loss_entropy):惩罚权重过于集中(希望不要太偏)
损失函数形式:
# ✅ 最终输出
1 | return(list(H = H, w = w)) |
H:最终的集成相似度矩阵(可用于后续聚类)w:每个方法的权重(代表各自的可靠程度)
# 🎯 总结一句话:
solve_ensemble用自适应的 soft weighting 方式,把多个二值聚类矩阵集成成一个更稳定、更综合的相似性矩阵,并学出每个方法的相对权重。
# 🚀 应用场景
- 多模型聚类集成(比如图聚类、谱聚类、k-means 等)
- 空间转录组多模态数据整合
- 图神经网络中的邻接矩阵集成
- 任意相似度矩阵融合场景
如果你有具体的 Results.clustering 示例或者想接着看看后续聚类操作(比如怎么从 H 得到最终的 cluster label),我也可以帮你对接上~
# weighted_average
1 | weighted_average <- function(x, w){ |
weighted_average
这段 R 代码定义了一个函数 weighted_average ,它的作用是:计算矩阵 x 中非零元素的加权平均(不做归一化),即仅在非零元素上对 x 和权重 w 做加权求和。
我们来逐步分析它做了什么:
# ✅ 函数功能分解:
1 | weighted_average <- function(x, w){ |
x: 一个矩阵或向量,包含原始数值(如某些度量、得分、相似度等)w: 和x相同维度的权重矩阵 / 向量
# 1. 提取非零位置:
1 | index_non_zero <- which(x != 0, arr.ind = TRUE) |
which(x != 0):找到x中非零元素的索引arr.ind = TRUE:如果x是矩阵,返回二维下标(行列索引),而不是扁平化的一维索引
# 2. 获取对应的非零值和权重:
1 | x_use <- x[index_non_zero] |
- 提取
x中非零元素的位置 - 并提取对应的权重
# 3. 加权求和:
1 | results <- sum(x_use * w_use) |
- 直接把
x的非零值与对应权重相乘后求和
❗注意:这个不是标准的 “加权平均”(没有除以权重总和),更准确说法是 “加权和”。
# 4. 返回值:
1 | return(results) |
# ✅ 举个例子:
1 | x <- matrix(c(0, 1, 2, 0), nrow = 2) |
非零位置是:
1 | [1,2] = 1 对应权重 = 0.4 |
结果是:
1 | 1*0.4 + 2*0.2 = 0.4 + 0.4 = 0.8 |
# 🧠 总结:
这个函数常用于:
- 对相似度矩阵等稀疏数据,在非零区域进行加权处理
- 某些 “mask”-like 或 “边权”-like 结构(如图中的边权重加权)
如果你想要做标准化的加权平均,可以在最后加一行:
1 | results <- sum(x_use * w_use) / sum(w_use) |
要不要我帮你改成这个形式?或者说你是在哪个上下文中用这个函数的?我可以帮你判断是不是少了归一化。
# patch_deal
1 | ########### ensemble strategy ########### |
patch_deal
这段 R 代码的核心功能是:
将用户自定义聚类结果(
clustering_df)转化为相应的相似度矩阵,并整合到已有的聚类结果列表res中,作为扩展后的 ensemble 输入。
下面是详细分析:
# 🔧 函数定义和参数
1 | patch_deal <- function(res, clustering_df) |
# 参数说明:
res:一个列表,结构是res[[1]]为聚类标签列表(每个方法一个向量),res[[2]]为相应的 spot-spot 相似度矩阵(如 0-1 表示同聚类)。clustering_df:用户自己运行的聚类结果,每列是一种方法的聚类标签,每行是一个 spot。
# 🧩 代码解析步骤:
# 1. 检查聚类列名:
1 | if(is.null(colnames(clustering_df))) |
要求 clustering_df 的每列命名为方法名。
# 2. 初始化和准备变量:
1 | res.final = res |
# 3. 按照已有顺序对 clustering_df 进行重排:
1 | clustering_df = clustering_df[spot_names, ] |
确保 clustering_df 中的行顺序和 res 中的顺序一致。
# 4. 主循环:将用户的聚类标签转为 similarity matrix
1 | for (i in 1:n_path) { |
# 🚩这里调用了你之前的函数:
1 | clust2Mat <- function(memb){ |
该函数把聚类标签向量变成了一个 binary similarity matrix,元素为 1 表示属于同一个聚类,主对角线为 0。
# 5. 更新方法名:
1 | names(res.final[[1]]) = names_all |
添加新方法后重新标记所有方法名。
# ✅ 返回值:
1 | return(res.final) |
这个 res.final 是完整更新过的 ensemble 输入,包含基础方法 + 用户方法的聚类标签和 similarity 矩阵。
# 🔁 总结图示
1 | clustering_df: |
如果你希望我可视化一下这种 “聚类 → similarity 矩阵” 的转化,我也可以画一个示意图。要不要?
# plot_Sankey
1 | # data = read.table("C:/data/Vandy Onedrive/OneDrive - Vanderbilt/Desktop/Coranl_df.txt") |
Sankey
这段 R 语言代码 的主要功能是:** 根据多个聚类(cluster)之间的对应关系,绘制 Sankey 图(桑基图)来可视化聚类之间的映射关系变化。** 下面是对每个部分的逐步解释。
# 🔧 1. create_df_Sankey 函数
功能:生成一个二维的频次矩阵,表示 cluster1 和 cluster2 中各个类别之间的映射频率。
# 参数:
cluster1:第一列聚类标签向量cluster2:第二列聚类标签向量
# 过程:
1 | for(i in 1:length(levels1)){ |
遍历 cluster1 中的每个类别( level1[i] )和 cluster2 中的每个类别( level2[j] ),统计有多少个样本从 cluster1 == level1[i] 映射到了 cluster2 == level2[j] 。
# 返回值:
一个 频次矩阵(行是 cluster1 的类别,列是 cluster2 的类别)。
# 📊 2. plot_sankey_fun 函数
功能:根据传入的 links 数据框,绘制 Sankey 图。
# 输入:
links 是一个 data.frame,包含三列:
source: 源节点(字符串)target: 目标节点(字符串)value: 权重或频次
# 关键步骤:
1 | nodes <- data.frame(name = unique(c(as.character(links$source), as.character(links$target)))) |
生成唯一节点名,构成节点表。
1 | links$IDsource <- match(links$source, nodes$name) - 1 |
把 source 和 target 映射为 0-based 的整数 ID,这是 networkD3::sankeyNetwork() 要求的格式。
# 🌉 3. plot_sankey 函数(主函数)
功能:整合多个聚类层次之间的关系,绘制一张完整的 Sankey 图。
# 参数:
df:一个 data frame,行表示样本,列表示不同的聚类(cluster)结果。filter:过滤阈值,小于这个频次的映射不展示。
# 过程详解:
# Step 1:两两列之间调用 create_df_Sankey :
1 | for (i in 1:(ncol(df)-1)) { |
生成 i 和 i+1 列之间的频次关系矩阵。
# Step 2:为了避免节点名冲突,为每个节点加上前缀:
1 | level_row <- paste0('Domain', length(levels(as.factor(df[,i]))), '_', rownames(tmp1)) |
# Step 3:使用 reshape2::melt 把矩阵转换成长格式,并过滤:
1 | tmp2 <- reshape2::melt(tmp1) |
转换成包含三列(source, target, value)形式,去掉低频连接。
# Step 4:汇总所有连接信息到 links :
1 | source_sk <- c(source_sk, as.character(df_list[[j]][,1])) |
最终构建:
1 | links <- data.frame(source=source_sk, target=target_sk, value=values_sk) |
# Step 5:调用 plot_sankey_fun() 绘图。
# 📌 总结
这段代码的用途是在有多个层次聚类标签的情况下,比如:
| cluster1 | cluster2 | cluster3 |
|---|---|---|
| A | X | L |
| A | Y | M |
| B | X | L |
| B | Y | N |
它将展示从 cluster1 → cluster2 → cluster3 的路径关系图,并用 Sankey 图 形式可视化流动和分布情况(常见于 单细胞聚类可视化,也可用于任何类别映射追踪)。
如果你有这个函数的实际数据样例或者想绘制的聚类结果,我也可以帮你进一步分析或展示可视化结果。