DeepST: identifying spatial domains in spatial transcriptomics by deep learning

# Abstract

DeepST can dissect spatial domains in cancer tissue at a finer scale.

DeepST can not only effective batch integration of ST data generated from multiple batches or different technologies, but also epandeable capabilities for processing other spatial omics data.

DeepST has the exceptional capacity for identifying spatial domains, making it a desirable tool to gain novel insights from ST studies.

# 使用 DeepSeek 生成的文章概要：

这篇文章介绍了一个名为 DeepST 的深度学习框架，用于在空间转录组学（Spatial Transcriptomics, ST）中识别空间域（spatial domains）。以下是文章的主要内容和关键点：

# 1. 背景与动机

• 空间转录组学（ST）技术（如 10x Visium、Slide-seq、Stereo-seq 等）能够在原位（in situ）水平上理解组织的功能和细胞结构。
• 识别空间域（即基因表达和组织学在空间上一致的区域）是空间转录组学中的一个重要课题。
• 现有的方法主要分为两类：非空间聚类方法（如 K-means、Louvain）和空间聚类方法（如 BayesSpace、stLearn、SpaGCN、SEDR）。这些方法虽然能够识别空间域，但通常依赖于线性主成分分析（PCA），无法捕捉复杂的非线性关系，且在批处理效应校正和处理其他空间组学数据方面存在局限性。

# 2. DeepST 的提出

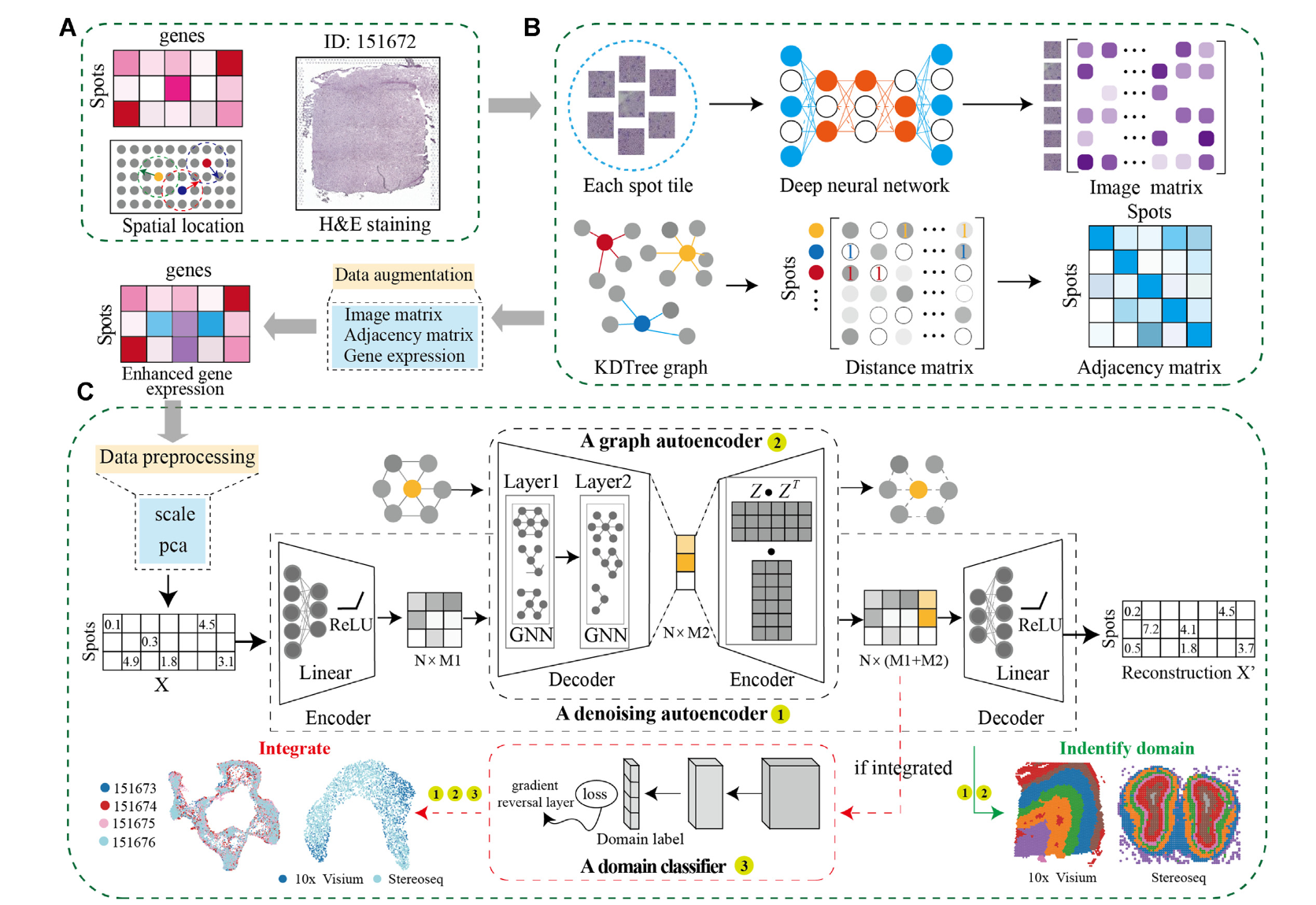
• DeepST 是一个基于深度学习的框架，旨在准确识别空间域。它通过结合基因表达、空间位置和组织形态学信息来增强空间域识别的准确性。
• DeepST 使用预训练的深度神经网络模型从形态学图像中提取特征向量，并将这些特征与基因表达和空间位置数据结合，生成一个增强的基因表达矩阵。
  • DeepST extracts feature vectors from morphological image tiles using a pre-trained deep neural network model, then integrates the extracted features with gene expression and spatial location data to characterize the correlation of spatially adjacent spots, and creates a spatial augment gene expression matrix.
• DeepST 使用图神经网络（GNN）自动编码器和去噪自动编码器来生成潜在表示，并通过域对抗神经网络（DAN）来整合来自多个批次或不同技术的 ST 数据。
  • DeepST uses a graph neural network (GNN) autoencoder and a denoising autoencoder to jointly generate a latent representation of augmented ST data, while domain adversarial neural networks(DAN) are used to integrate ST data from multiple batches or different technologies.

# 3. 方法与实现

# 数据预处理：

DeepST 首先从 ST 数据中提取形态学特征，并使用 PCA 降维。然后，它通过计算基因表达相似性、形态学相似性和空间邻居关系来增强基因表达。
Correlation $\textbf_{ij}$ was applied to calculate the weights of saptial gene expression between spot $\textbf{S}_i$ and spot $\textbf{S}_j$ as:

\begin{align} \textbf{GC}_{ij}=1-\frac{(\textbf{S}_i-\bar{\textbf{S}_i})\cdot(\textbf{S}_j-\bar{\textbf{S}_j})}{||(\textbf{S}_i-\bar{\textbf{S}_i})||_2\cdot||(\textbf{S}_j-\bar{\textbf{S}_j})||_2} \end{align}

这里是在计算它的余弦相似性

对于 morphological information 我们将图片进行切割，并通过标准化、旋转、调整锐度等方式增强图片。high--level features 通过一个预训练的神经网络提取。通过 PCA 操作提取 50 个特征。Finally, the weights of morphological similarity $\textbf{MS}_{ij}$ between spot $\textbf{S}_i$ and adjacent spot $\textbf{S}_j$ were calculated using the cosine distance as:

\begin{align} \textbf{MS}_{ij}=1-\frac{\textbf{S}_i\cdot\textbf{S}_j}{||\textbf{S}_i||_2\cdot||\textbf{S}_j||_2} \end{align}

对于给定的半径范围，如果$\textbf{S}_i$ 和$\textbf{S}_j$ 是相邻的那么$\textbf{SW}_{ij}=1$ 反之等于$0$

DeepST then enhances gene expression $\tilde{GE}_i$ of ench spot $\textbf{S}_i$ incorporating gene expression correlation, spatial neighbour, and morphological similarity as:

\begin{align} \tilde{\textbf{GE}}_i=\textbf{GE}_i+\frac{\sum_{j=1}^n \textbf{GE}_j \cdot\textbf{MS}_{ij}\cdot\textbf{GC}_{ij}\cdot\textbf{SW}_{ij}}{n} \end{align}

if in 10 $\times$ Visium, otherwise as:

\begin{align} \tilde{\textbf{GE}}_i=\textbf{GE}_i+\frac{\sum_{j=1}^n \textbf{GE}_j \cdot\textbf{GC}_{ij}\cdot\textbf{SW}_{ij}}{n} \end{align}

where $\textbf{GE}_i$ and $\textbf{GE}_j$ are the raw gene expressions for spot $\textbf{S}_i$ and n adjacent spots $\textbf{S}_j$

# 图构建：

DeepST 使用空间坐标构建细胞 - 细胞空间关系图，并通过 GNN 进行图嵌入。

# 去噪自动编码器：

DeepST 使用去噪自动编码器来学习基因表达的非线性映射，减少模型过拟合。
DeepST implements a denoising autoencoder for the latent representation of gene expression using linear layers with PyTorch.The encoder E, which consists of multiple fully connected stacked linear layers as set by a user, converts the integrated gene expressions $X$(the PCA embeding of $\tilde{\textbf{GE}}_i$)into a low-dimensional representation $\textbf{Z}_g$ as:

\begin{align} E(\textbf{X})=\textbf{Z}_g,\textbf{X}\in R^{N\times M},\textbf{Z}_g\in R^{N\times R} \end{align}

where $N$ is the number of spots, $M$ is the number of input genes, and $R$ is the dimension of the last encoder layer. Conversely, the decoder $D$ reverses the latent representation and tries to reconstruct the original input as:

\begin{align} \textbf{Z}_{g'}=\textbf{Z}_g+\textbf{Z}, \\ D(\textbf{Z}_{g'}) = \textbf{X}',\textbf{Z}_{g'}\in R^{N\times (R+R')},\textbf{X}' \in R^{N\times M}, \\ \end{align}

The mean squared error is applied to determine how comparable the input gene and reconstructed expressions are as:

\begin{align} L_l=\frac{1}{N}\sum_{i=1}^N ||\textbf{X}_i-D(E(\textbf{X}_i))||^2 \end{align}

解释

在 DeepST 框架中，解码器（Decoder）的任务是从潜在表示中重构原始输入数据。公式：

\begin{align} \textbf{Z}_{g'} = \textbf{Z}_g + \textbf{Z}, \\ D(\textbf{Z}_{g'}) = \textbf{X}', \quad \textbf{Z}_{g'} \in \mathbb{R}^{N \times (R + R')}, \quad \textbf{X}' \in \mathbb{R}^{N \times M}, \end{align}

表示以下过程：

---

# 1. 潜在表示的融合

• $\textbf{Z}_g$：来自去噪自动编码器（Denoising Autoencoder）的潜在表示，维度为 $N \times R$，捕捉基因表达的非线性特征。
• $\textbf{Z}$：来自变分图自动编码器（VGAE）的潜在表示，维度为 $N \times R'$，捕捉空间依赖关系。
• $\textbf{Z}_{g'}$：两者的拼接（Concatenation），而非简单相加。实际应为：\begin{align} \textbf{Z}_{g'} = [\textbf{Z}_g; \textbf{Z}] \quad \text{（按列拼接）}, \end{align} 因此维度变为 $N \times (R + R')$。公式中的 “+” 可能是符号简化，实际表示联合两种潜在信息。

---

# 2. 解码器的重构过程

解码器 $D$ 是一个神经网络（如全连接层），其输入是联合潜在表示 $\textbf{Z}_{g'}$，目标是输出重构的基因表达矩阵 $\textbf{X}'$，维度为 $N \times M$（与原始输入 $\textbf{X}$ 一致）。

具体步骤：

1. 输入：联合潜在表示 $\textbf{Z}_{g'} \in \mathbb{R}^{N \times (R + R')}$。
2. 解码操作：通过线性或非线性层映射到原始空间：\begin{align} \textbf{X}' = D(\textbf{Z}_{g'}) = \text{Decoder}(\textbf{Z}_{g'}). \end{align}
3. 目标：最小化重构误差（如均方误差）：\begin{align} L_{\text{recon}} = \frac{1}{N} \sum_{i=1}^N \|\textbf{X}_i - \textbf{X}'_i\|^2. \end{align}

---

# 3. 符号澄清

• “+” 的真实含义：在大多数深度学习框架中，维度不同的张量无法直接相加。因此，公式中的 “+” 更可能是拼接（Concatenation），而非逐元素加法。这符合维度从 $R$ 和 $R'$ 扩展为 $R + R'$ 的描述。
• 维度一致性：
  • $\textbf{Z}_g \in \mathbb{R}^{N \times R}$，$\textbf{Z} \in \mathbb{R}^{N \times R'}$。
  • 拼接后 $\textbf{Z}_{g'} \in \mathbb{R}^{N \times (R + R')}$。
  • 解码器 $D$ 将其映射到 $\textbf{X}' \in \mathbb{R}^{N \times M}$，恢复原始基因表达维度。

---

# 4. 重构的意义

• 特征融合：通过拼接 $\textbf{Z}_g$（基因表达特征）和 $\textbf{Z}$（空间特征），解码器能够综合两种信息，生成更准确的基因表达重构。
• 去噪与泛化：重构过程迫使模型学习数据中的关键模式，忽略噪声（尤其在去噪自动编码器中）。
• 空间一致性：图自动编码器的潜在表示 $\textbf{Z}$ 编码了空间邻域关系，确保重构的基因表达在空间上连贯。

---

# 5. 示例说明

假设：

• 原始基因表达数据 $\textbf{X} \in \mathbb{R}^{1000 \times 5000}$（1000 个点，5000 个基因）。
• $\textbf{Z}_g \in \mathbb{R}^{1000 \times 50}$（去噪自动编码器的 50 维潜在表示）。
• $\textbf{Z} \in \mathbb{R}^{1000 \times 30}$（图自动编码器的 30 维潜在表示）。

则：

• 拼接后 $\textbf{Z}_{g'} \in \mathbb{R}^{1000 \times 80}$。
• 解码器 $D$ 将其映射到 $\textbf{X}' \in \mathbb{R}^{1000 \times 5000}$，逼近原始数据。

---

# 6. 总结

该公式描述了 DeepST 中如何通过联合两种潜在表示（基因表达和空间信息），并利用解码器重构原始输入数据。重构过程通过最小化误差，使模型能够有效融合多源信息，提升空间域识别的准确性。公式中的 “+” 实际应为拼接操作，确保不同来源的特征得以整合。

# 变分图自动编码器：

DeepST 使用变分图自动编码器来捕捉空间关联，生成空间嵌入。
Variational Graph Autoencoder (VGAE) 是一种基于图神经网络（Graph Neural Network, GNN）的变分自动编码器（Variational Autoencoder, VAE），专门用于处理图结构数据。在 DeepST 中，VGAE 被用来捕捉空间转录组数据中的空间依赖关系，并生成潜在的空间嵌入表示。以下是 VGAE 的详细说明：

---

# 1. VGAE 的基本结构

VGAE 由两个主要部分组成：

• 编码器（Encoder）：将输入的图数据（如基因表达数据和空间邻接矩阵）映射到一个低维的潜在空间。
• 解码器（Decoder）：从潜在空间中重构原始的图结构（如邻接矩阵）。

VGAE 的核心思想是通过变分推断（Variational Inference）来学习潜在表示，从而捕捉数据中的非线性关系和不确定性。

---

# 2. 编码器（Encoder）

编码器的作用是将输入的图数据映射到潜在空间。在 VGAE 中，编码器通常由两层图神经网络（GNN）组成，具体步骤如下：

# 2.1 输入数据

• 特征矩阵 $\textbf{X}$：表示每个节点的特征（如基因表达数据）。在 DeepST 中，$\textbf{X}$ 是经过 PCA 降维后的基因表达数据。
• 邻接矩阵 $\textbf{A}$：表示节点之间的空间关系（如空间邻接关系）。在 DeepST 中，$\textbf{A}$ 是通过空间坐标构建的邻接矩阵。

# 2.2 图神经网络（GNN）

编码器使用 GNN 来提取节点的特征表示。具体来说，GNN 通过聚合邻居节点的信息来更新每个节点的表示。公式如下：

\begin{align} \hat{\textbf{X}} = \text{GNN}(\textbf{X}, \textbf{A}) = \hat{\textbf{A}} \cdot \text{ReLU}(\hat{\textbf{A}} \cdot \textbf{X} \cdot \textbf{W}_0) \cdot \textbf{W}_1 \end{align}

其中：

• $\hat{\textbf{A}} = \textbf{D}^{-1/2} \textbf{A} \textbf{D}^{-1/2}$ 是归一化的邻接矩阵（对称归一化），$\textbf{D}$ 是度矩阵。
• $\textbf{W}_0$ 和 $\textbf{W}_1$ 是可学习的权重矩阵。
• ReLU 是激活函数。

# 2.3 生成潜在表示

编码器的最后一层生成潜在表示的均值和方差：

\begin{align} \mu = \text{GNN}_{\mu}(\textbf{X}, \textbf{A}) = \hat{\textbf{A}} \cdot \textbf{X} \cdot \textbf{W}_2 \end{align} \begin{align} \log \sigma^2 = \text{GNN}_{\sigma}(\textbf{X}, \textbf{A}) = \hat{\textbf{A}} \cdot \textbf{X} \cdot \textbf{W}_2 \end{align}

其中：

• $\mu$ 是潜在表示的均值。
• $\log \sigma^2$ 是潜在表示的方差的对数。
• $\textbf{W}_2$ 是可学习的权重矩阵。

# 2.4 重参数化技巧（Reparameterization Trick）

为了从潜在分布中采样，VGAE 使用重参数化技巧：

\begin{align} \textbf{Z} = \mu + \log \sigma^2 * \epsilon \end{align}

其中：

• $\epsilon \sim \mathcal{N}(0, 1)$ 是从标准正态分布中采样的噪声。
• $\textbf{Z}$ 是最终的潜在表示。

---

# 3. 解码器（Decoder）

解码器的作用是从潜在表示 $\textbf{Z}$ 中重构原始的图结构（如邻接矩阵）。在 VGAE 中，解码器通常是一个简单的内积操作：

\begin{align} p(\textbf{A}|\textbf{Z}) = \prod_{i=1}^N \prod_{j=1}^N p(\textbf{A}_{ij}|z_i, z_j) \end{align}

其中：

• $p(\textbf{A}_{ij} = 1|z_i, z_j) = \sigma(\textbf{Z} \textbf{Z}^T)$ 是节点 $i$ 和节点 $j$ 之间存在边的概率。
• $\sigma(\cdot)$ 是逻辑 sigmoid 函数。

---

# 4. 损失函数

VGAE 的损失函数由两部分组成：

1. 重构损失（Reconstruction Loss）：衡量解码器重构的邻接矩阵与原始邻接矩阵之间的差异。
2. KL 散度（Kullback-Leibler Divergence）：衡量潜在表示 $\textbf{Z}$ 的分布与标准正态分布之间的差异。

具体公式如下：

\begin{align} L_s = \mathbb{E}_{q(\textbf{Z}|\textbf{X}, \textbf{A})}[\log p(\textbf{A}|\textbf{Z})] - \text{KL}[q(\textbf{Z}|\textbf{X}, \textbf{A}) || p(\textbf{Z})] \end{align}

其中：

• $\mathbb{E}_{q(\textbf{Z}|\textbf{X}, \textbf{A})}[\log p(\textbf{A}|\textbf{Z})]$ 是重构损失，通常使用二元交叉熵（Binary Cross-Entropy）计算。
• $\text{KL}[q(\textbf{Z}|\textbf{X}, \textbf{A}) || p(\textbf{Z})]$ 是 KL 散度，用于正则化潜在表示 $\textbf{Z}$ 的分布。

---

# Clustering metrics

Silhouette Coefficient(SC) score: SC is calculated using the mean intra-cluster distance a and the mean nearest-cluster distance b for each sample. For a sample is (b-a)/max(a,b), and the best value is 1 and the worst value is -1.

Davies-Bouldin(DB) score: DB is defined as the average similarity is the ratio of within its most similar cluster, where similarity is the ratio of wothin-cluster distance to between cluster distances. The minimum score is zero, with lower values indicating better clustering.

Metrics

# Silhouette Coefficient Score（轮廓系数）

# 定义与目的

轮廓系数用于评估聚类结果的质量，衡量样本在所属簇中的紧密度（Cohesion）与与其他簇的分离度（Separation）。其值范围在 [-1, 1]：

• 接近 1：样本被正确分配到紧密且分离良好的簇。
• 接近 0：样本位于簇的边界区域。
• 接近 -1：样本可能被分配到错误的簇。

# 计算公式

对单个样本 $i$：

\begin{align} s(i) = \frac{b(i) - a(i)}{\max\{a(i), b(i)\}} \end{align}

• $a(i)$：样本 $i$ 到同簇其他样本的平均距离（反映簇内紧密度）。
• $b(i)$：样本 $i$ 到其他簇中所有样本的平均距离的最小值（反映与其他簇的分离度）。

整体轮廓系数是所有样本得分的平均值：

\begin{align} \text{Silhouette Score} = \frac{1}{N} \sum_{i=1}^N s(i) \end{align}

# 特点与适用场景

• 优点：直观，适用于无标签数据；能同时评估紧密度和分离度。
• 缺点：计算复杂度高（需计算所有样本间距离）；对凸形簇敏感。
• 应用：对比不同聚类算法或参数的效果（如 K-means 中选择最佳 K 值）。

---

# Davies-Bouldin Score（戴维森堡丁指数）

# 定义与目的

Davies-Bouldin 指数衡量聚类结果的簇内紧密度与簇间分离度的综合质量，其值越小越好（理想值为 0）：

• 低值：簇内紧密，簇间分离清晰。
• 高值：簇内松散或簇间重叠严重。

# 计算公式

1. 簇内紧密度：通常用簇中所有样本到质心的平均距离表示，记为 $S_i$。
2. 簇间分离度：两簇质心间的距离，记为 $d_{ij}$。
3. 相似度：对簇 $i$，计算与其他簇 $j$ 的相似度：

\begin{align} R_{ij} = \frac{S_i + S_j}{d_{ij}} \end{align}

4. 簇 $i$ 的最差相似度：取 $R_{ij}$ 的最大值 $R_i = \max_{j \neq i} R_{ij}$。
5. 整体指数：所有簇 $R_i$ 的平均值：

\begin{align} \text{DB Score} = \frac{1}{K} \sum_{i=1}^K R_i \end{align}

# 特点与适用场景

• 优点：计算高效（仅需质心信息）；对簇形状无假设。
• 缺点：对簇大小和密度差异敏感；可能低估非凸簇的效果。
• 应用：快速评估聚类质量，适用于大规模数据集。

---

# 对比与选择建议

指标	轮廓系数	Davies-Bouldin 指数
值范围	[-1, 1]，越大越好	[0, +∞)，越小越好
计算复杂度	高（需所有样本间距离）	低（仅需质心信息）
对簇形状的敏感性	对凸形簇敏感	对任意形状簇通用
适用场景	小规模数据，需详细分析聚类质量	大规模数据，快速评估

# 选择建议

• 若需直观评估样本级别的聚类质量，优先选择轮廓系数。
• 若数据规模大或需快速比较算法，选择 Davies-Bouldin 指数。
• 在空间转录组学中（如 DeepST），两者可结合使用：轮廓系数评估局部区域一致性，Davies-Bouldin 指数衡量全局结构。

---

# 示例

假设对空间转录组数据应用 K-means 聚类（K=5）：

• 轮廓系数 = 0.6：表明样本在簇内紧密，簇间分离良好。
• Davies-Bouldin 指数 = 0.3：进一步验证聚类质量高。

若调整 K 值后，轮廓系数下降至 0.2，Davies-Bouldin 指数上升至 1.5，则说明当前 K 值不理想。

graph和denoise的联系

在 DeepST 框架中，Denoising Autoencoder（DAE） 和 Variational Graph Autoencoder（VGAE） 是协同工作的两个核心组件，它们的联系主要体现在以下三个方面：

---

# 1. 功能互补：数据鲁棒性与空间依赖性

• Denoising Autoencoder
  负责处理基因表达数据，通过引入噪声并强制模型重构原始数据，增强基因表达的鲁棒性。其核心任务是：

  • 去除基因表达中的技术噪声（如测序误差）。
  • 提取非线性特征，捕捉基因间的复杂关系。
  • 公式：\begin{align} L_{\text{recon}} = \frac{1}{N} \sum_{i=1}^N \|\textbf{X}_i - D(E(\tilde{\textbf{X}}_i))\|^2 \end{align} 其中 $\tilde{\textbf{X}}_i$ 是加噪后的输入。

• Variational Graph Autoencoder
  负责处理空间邻接矩阵，捕捉空间依赖性（如相邻点在基因表达和组织形态上的相似性）。其核心任务是：

  • 通过图卷积网络（GNN）编码空间邻域关系。
  • 生成潜在表示 $\textbf{Z}$，反映空间一致性。
  • 公式（含 KL 散度和重构损失）：\begin{align} L_s = \mathbb{E}_{q(\textbf{Z}|\textbf{X}, \textbf{A})}[\log p(\textbf{A}|\textbf{Z})] - \text{KL}[q(\textbf{Z}|\textbf{X}, \textbf{A}) || p(\textbf{Z})] \end{align}

---

# 2. 潜在表示的联合与融合

两者的潜在表示通过拼接（Concatenation） 结合，形成综合的嵌入表示，用于下游任务（如空间域识别）：

\begin{align} \textbf{Z}_{g'} = [\textbf{Z}_g; \textbf{Z}] \end{align}

• $\textbf{Z}_g \in \mathbb{R}^{N \times R}$: DAE 的潜在表示（基因表达特征）。
• $\textbf{Z} \in \mathbb{R}^{N \times R'}$: VGAE 的潜在表示（空间特征）。
• $\textbf{Z}_{g'} \in \mathbb{R}^{N \times (R + R')}$: 联合表示，同时编码基因表达和空间信息。

这种融合使模型能够：

• 在基因表达中融入空间上下文（如相邻点的相似性）。
• 在空间结构中嵌入基因表达模式（如肿瘤区域的分子异质性）。

---

# 3. 联合训练与损失函数

DAE 和 VGAE 在训练过程中通过联合优化实现协同：

• 总损失函数：\begin{align} L_{\text{total}} = L_{\text{recon}} + \lambda L_s + L_{\text{DAN}} \end{align}
  • $L_{\text{recon}}$: DAE 的重构损失。
  • $L_s$: VGAE 的损失（含 KL 散度和邻接矩阵重构损失）。
  • $L_{\text{DAN}}$: 域对抗网络（Domain Adversarial Network）的损失（用于多批次数据整合）。
  • $\lambda$: 超参数，平衡不同任务的权重。

训练流程：

1. DAE 和 VGAE 分别提取基因表达和空间特征。
2. 联合潜在表示 $\textbf{Z}_{g'}$ 被输入解码器，重构基因表达矩阵 $\textbf{X}'$。
3. 通过最小化总损失，模型同时优化数据去噪、空间依赖建模和多批次整合。

---

# 4. 实际应用中的协同效果

• 空间域识别：DAE 的鲁棒基因特征与 VGAE 的空间一致性特征结合，使 DeepST 能更精确地划分复杂组织中的空间域（如区分肿瘤微环境中的亚区域）。
• 批效应校正：通过域对抗网络（DAN），联合表示 $\textbf{Z}_{g'}$ 进一步消除不同实验批次或平台的技术差异。
• 可扩展性：DAE 和 VGAE 的模块化设计允许处理其他空间组学数据（如 MERFISH、4i）。

---

# 总结

在 DeepST 中，DAE 和 VGAE 通过功能互补、潜在表示融合与联合训练，共同实现了：

1. 鲁棒基因特征提取（DAE）。
2. 空间依赖建模（VGAE）。
3. 多源数据整合（联合表示 + DAN）。

这种协同机制是 DeepST 在空间转录组分析中优于传统方法（如 PCA + 非深度学习模型）的关键创新点。

# Clustering and visualization

使用 leiden 作为 DeepST embeddings 的基础。

用 Calinski and Harabasz (CH) score 作为选取分辨率的标准，并采用最大的那个

可视化直接用 UMAP。

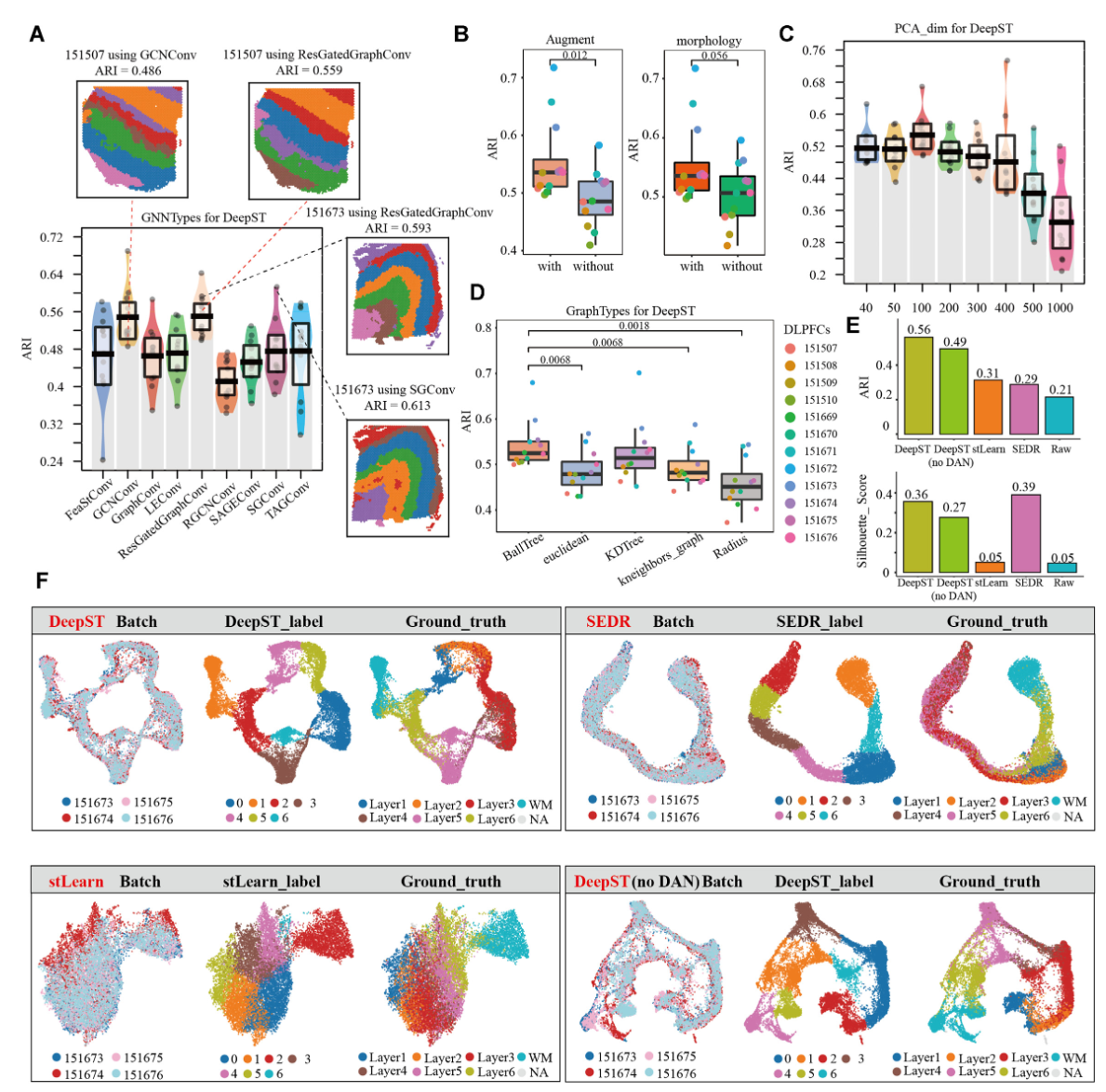
这里是消融实验和与其他方法的对比。

这里的 DAN 解决批次问题可以参考一下。

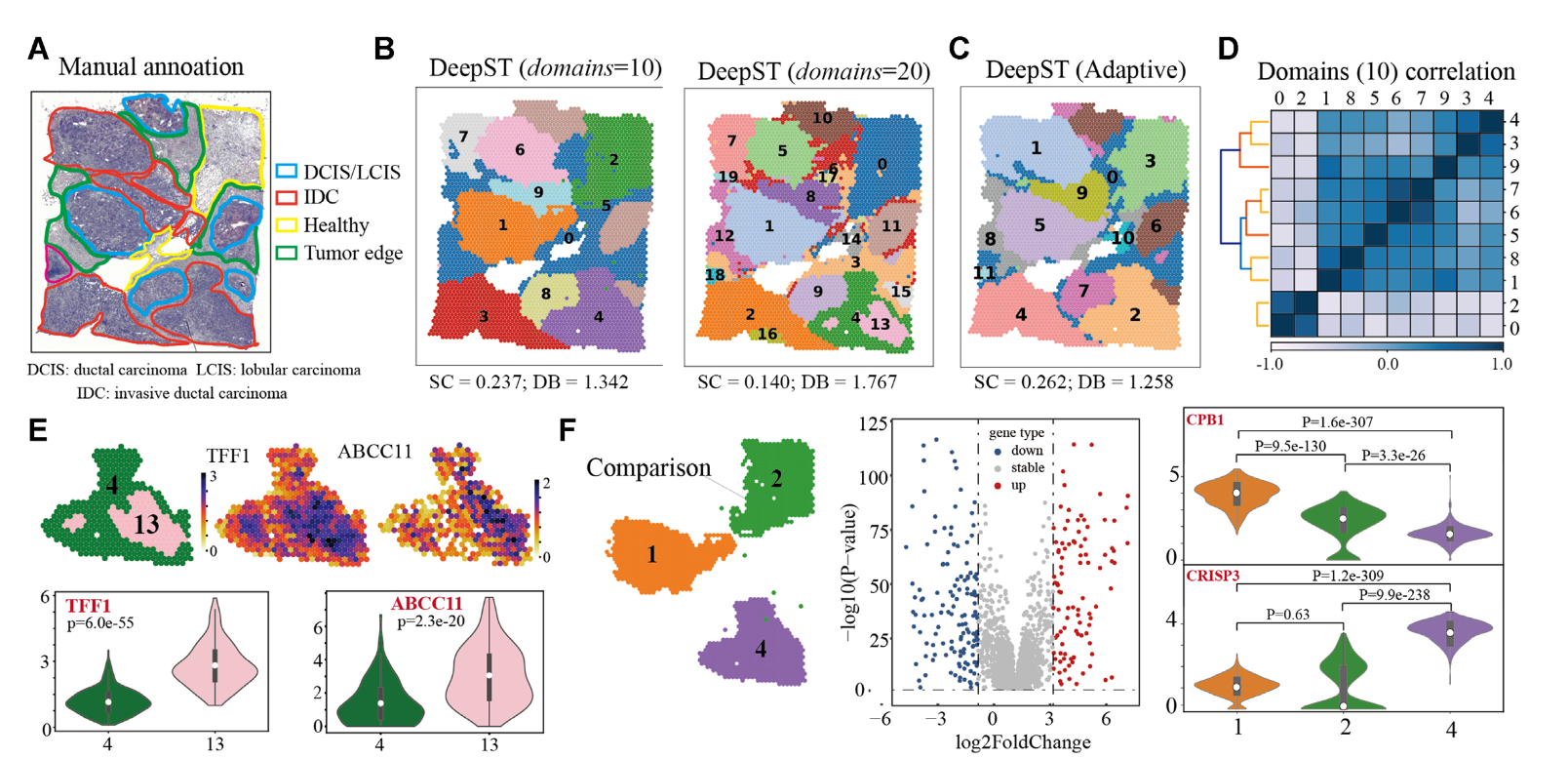
Spatial domains with hogh heterogeneity, anmely tumor regions, are getting finer as parameters domain get bigger. Meanwhile, regions with low heterogeneity, such as healthy regions, still kept consistent regardless of clustering resolution, indicating good robustness of DeepST.
这里是从 gene distribution 出发去研究肿瘤的问题。

# 5. 在 DeepST 中的应用

在 DeepST 中，VGAE 被用来捕捉空间转录组数据中的空间依赖关系。具体步骤如下：

1. 输入数据：基因表达数据 $\textbf{X}$ 和空间邻接矩阵 $\textbf{A}$。
2. 编码器：通过 GNN 提取潜在表示 $\textbf{Z}$，捕捉空间依赖关系。
3. 解码器：从潜在表示 $\textbf{Z}$ 中重构邻接矩阵，用于验证模型的学习效果。
4. 损失函数：通过重构损失和 KL 散度优化模型参数。

---

# 6. 总结

VGAE 是一种强大的图结构数据建模工具，能够捕捉数据中的非线性关系和空间依赖关系。在 DeepST 中，VGAE 被用来生成潜在 V 的空间嵌入表示，从而帮助识别空间域。通过结合基因表达数据、空间位置信息和形态学特征，GAE 能够有效地提升空间转录组数据的分析能力。

# 域对抗神经网络：

DeepST 使用域对抗神经网络（DAN）来整合来自不同批次或平台的 ST 数据，减少技术差异带来的影响。
DAN includes feature extractor, and domain classifier.

The feateure extractor is composed of a joint linear layer and a graph neural network. We add a domain discriminator, which is connexted by a gradient reversal layer (GRL) in the middle.

A domain classification layer $G_d$ learns a function $G_f:Z'_g \to R^D$ that maps an example into a new $D$ dimensional representatio, and is parameterized by a matrix-vector pair $(W,b) \in R^{D\times m}\times R^D$:

\begin{align} G_d(x;W,b)=sigm(Wx+b), \end{align}

with sigma(a)=[\frac{1}{1+exp)-a_i}]^{|a|}_

\begin{align} L_d=-\frac{1}{N}\sum_i\sum^m_{d=1}D_{id}log({p_{id}}), \end{align}

Where $M$ is the number of domains,$D_{id}$ is the sign function, if the true label of sample $i$ is equal to d, take 1, otherwise take 0, and $p_{id}$ is the probability that the observed sample i belongs to category $d$

# 4. 实验结果

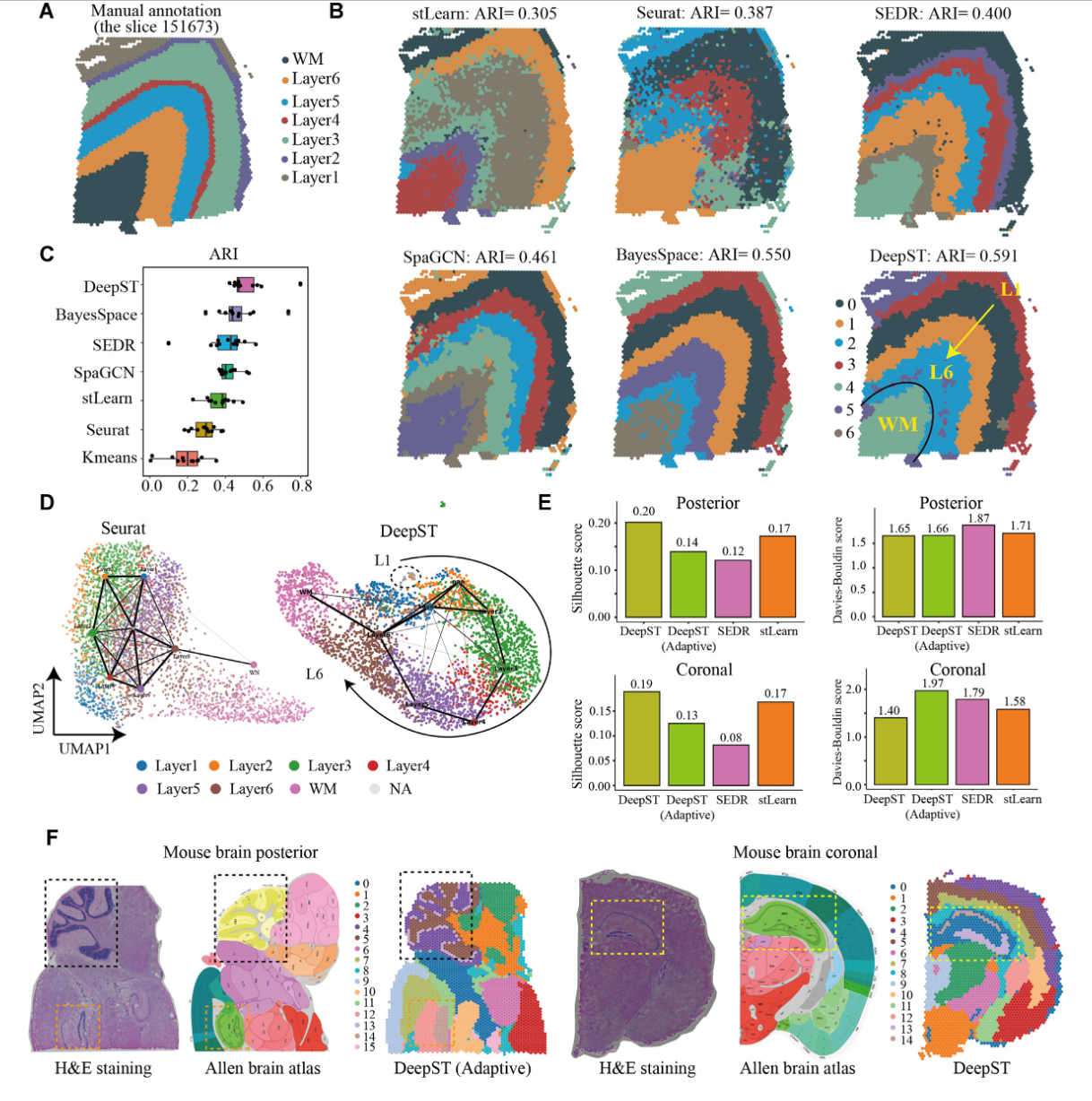
• 在人类前额叶皮层数据集上的表现：DeepST 在识别空间域方面优于现有的最先进方法（如 BayesSpace、SpaGCN、SEDR 等），尤其是在边界划分和层状结构的识别上表现出色。
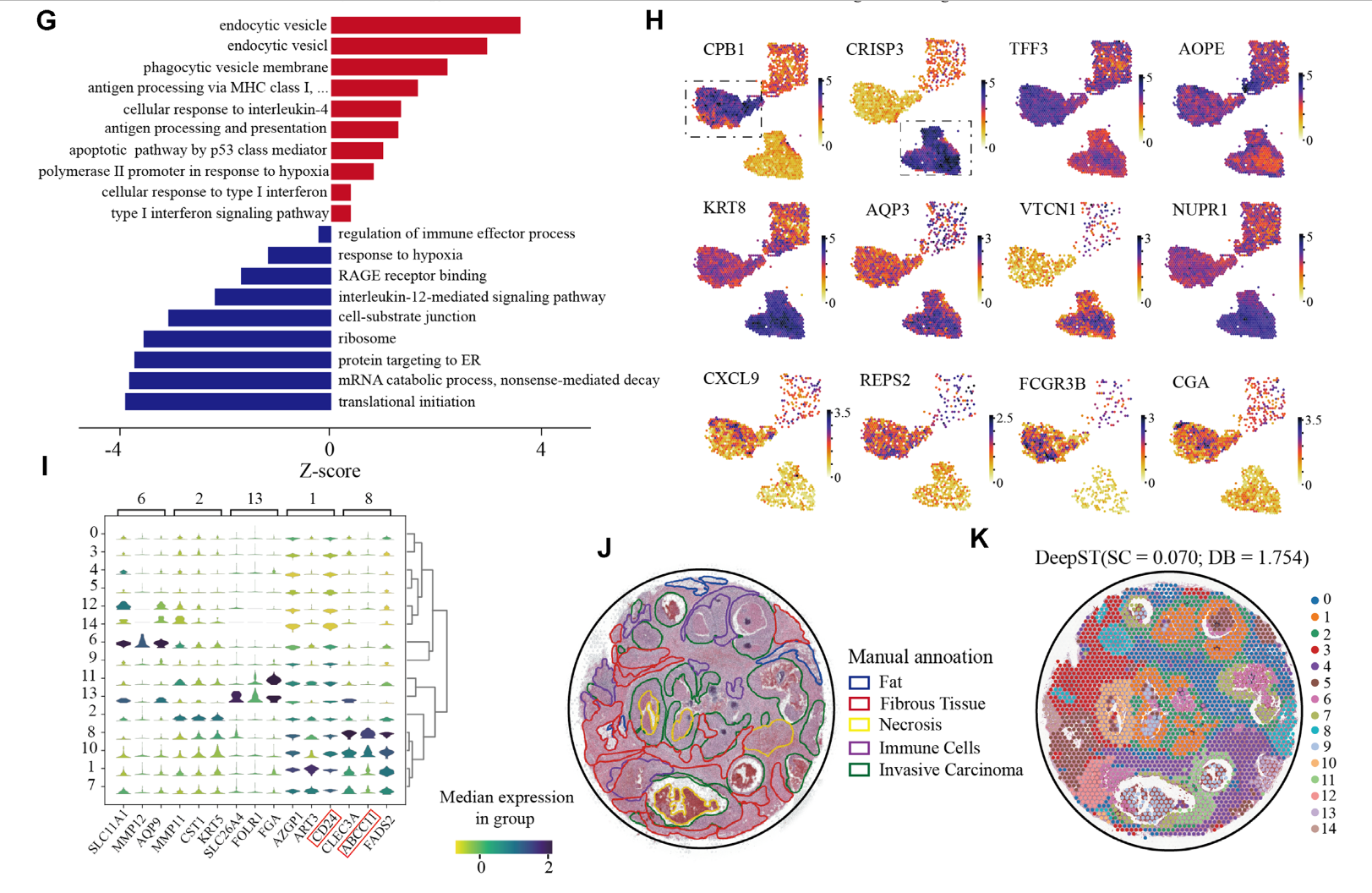
• 在乳腺癌数据集上的表现：DeepST 能够在癌症组织中识别出更细粒度的空间域，揭示了传统方法未能检测到的肿瘤异质性。
• 在其他空间组学数据上的表现：DeepST 不仅适用于 10x Visium 平台，还能够处理其他空间组学数据（如 MERFISH、4i、MIBI-TOF 等），并且在三维表达域的提取上也表现出色。

# 5. 讨论与未来工作

• DeepST 是一个灵活且高效的框架，能够处理多种空间组学数据，并且在识别空间域和校正批处理效应方面表现出色。
• 未来的工作可以集中在优化内存效率、整合空间组学和单细胞 RNA 测序数据，以及进一步提高模型的稳定性和收敛性。

# 6. 数据与代码可用性

• DeepST 的代码和详细教程可以在 GitHub 上获取：https://github.com/JiangBioLab/DeepST。
• 文章中使用的所有数据集均为公开数据集，可以从相关平台下载。

# 7. 结论

• DeepST 是一个强大的工具，能够通过整合基因表达、空间位置和组织形态学信息来识别空间域。随着更多 ST 数据的生成，DeepST 有望在空间背景下揭示细胞组织的新原理。

这篇文章通过详细的实验和对比，展示了 DeepST 在空间转录组学中的强大能力，尤其是在识别复杂组织中的空间域和处理多批次数据方面的优势。