Spatial transcriptomics at subspot resolution with BayesSpace

# Abstract

BayesSpace, a fully Bayesian statistical method that uses the information from spatial neighborhoods for resolution enhancement of spatial transcriptomic data and for clustering analysis.

we show that BayesSpace resolves tiissue structure that is not detectable at the original resolution and identifies transcriptional heterpgeneity inaccessible to histological analysis.

# Introduction

# Background

Single-cell RNA sequencing (scRNA-seq) achieves high-throughput and high-resolution profiling of gene expression, but because tissue is dissociated for sample preparation, spatial information is not retained.

Studies performed with the Spatial Transcriptomics (ST) platform and the improved Visium platform have already generated insights into diverse areas. The primary technological limitation of these spatial gene expression platforms is resolution, with the unit of observation being spots that are 100 μm in diameter on the ST platform and 55 μm in diameter on the Visium platform. As such, the number of cells within a spot may range from one to 30 on the Visium platform and up to 200 on the older ST platform, depending on the biological tissue.

Alternative approaches include fluorescence in situ hybridization (FISH) technologies, such as seqFISH and multiplexed error-robust FISH, and other recently developed spatial sequencing methods, such as Slide-seq and ZipSeq. While these methods provide increased resolution, most are lower throughput, less sensitive, rely on custom protocols or are not widely available.

# brief Method

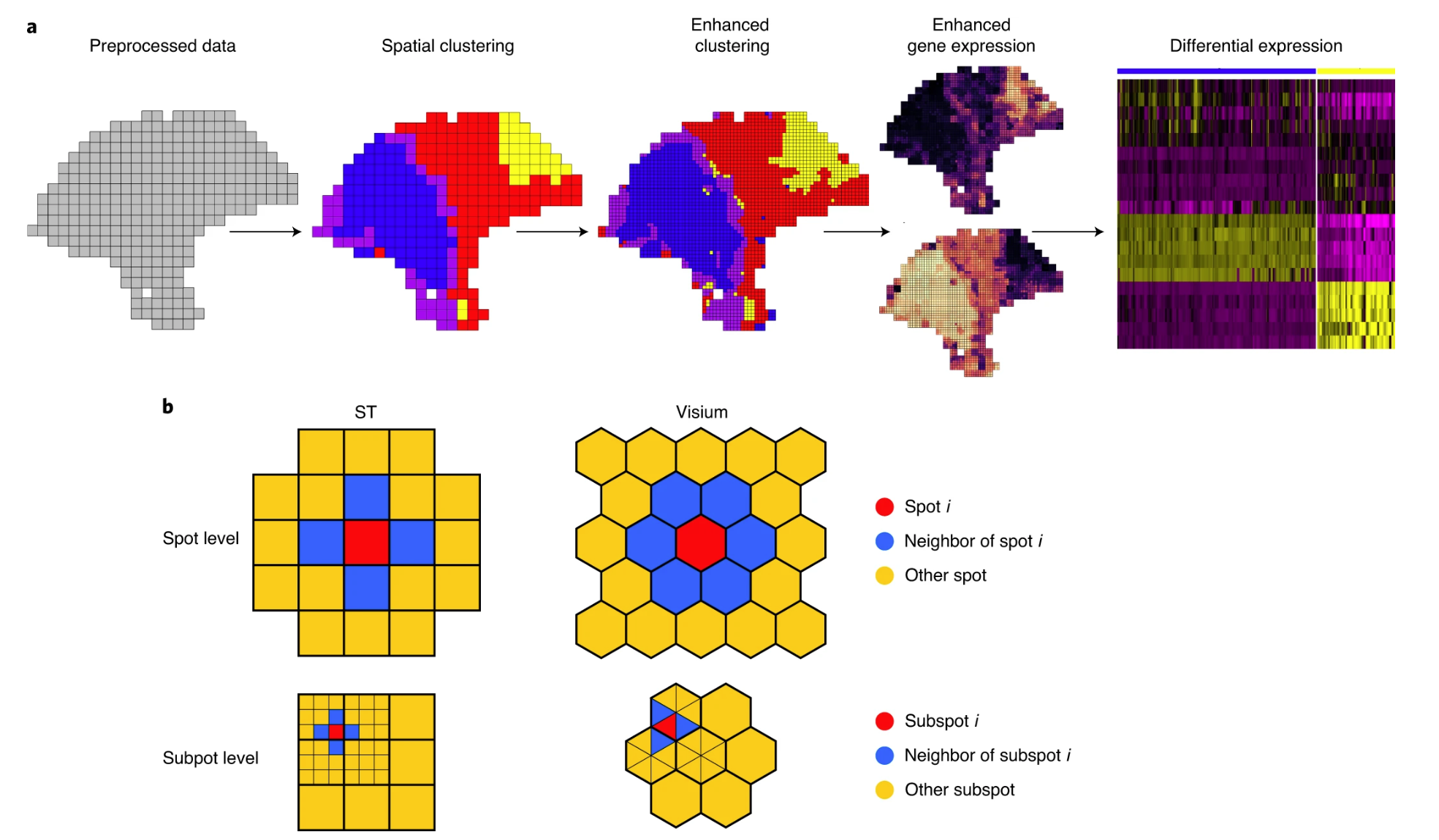
BayesSpace enables spatial clustering by modeling a low-dimensional representation of the gene expression matrix and encouraging neighboring spots to belong to the same cluster via a spatial prior.

Compared with previous approaches, BayesSpace allows for a more flexible specification of the clustering structure and error term than alternative spproaches.

BayesSpace improves the identification of spatially distributed tissue domains through spatial clustering and enhances the resolution of gene expression maps.

# Results

# Spatial clustering improves identification of known layers in brain tissues.

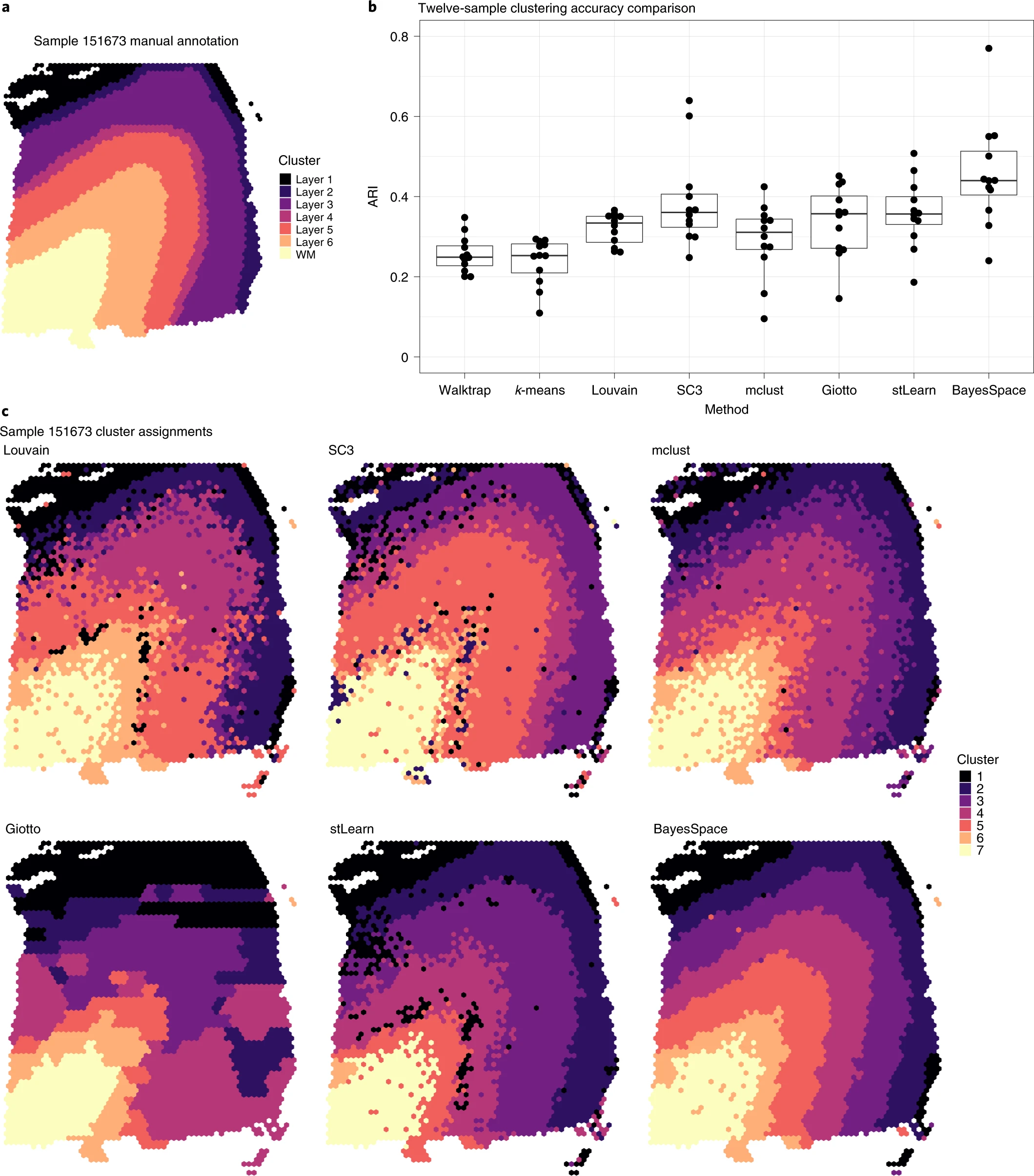
# Increased resolution clustering leads to identification of known tissue structures missed by other methods.

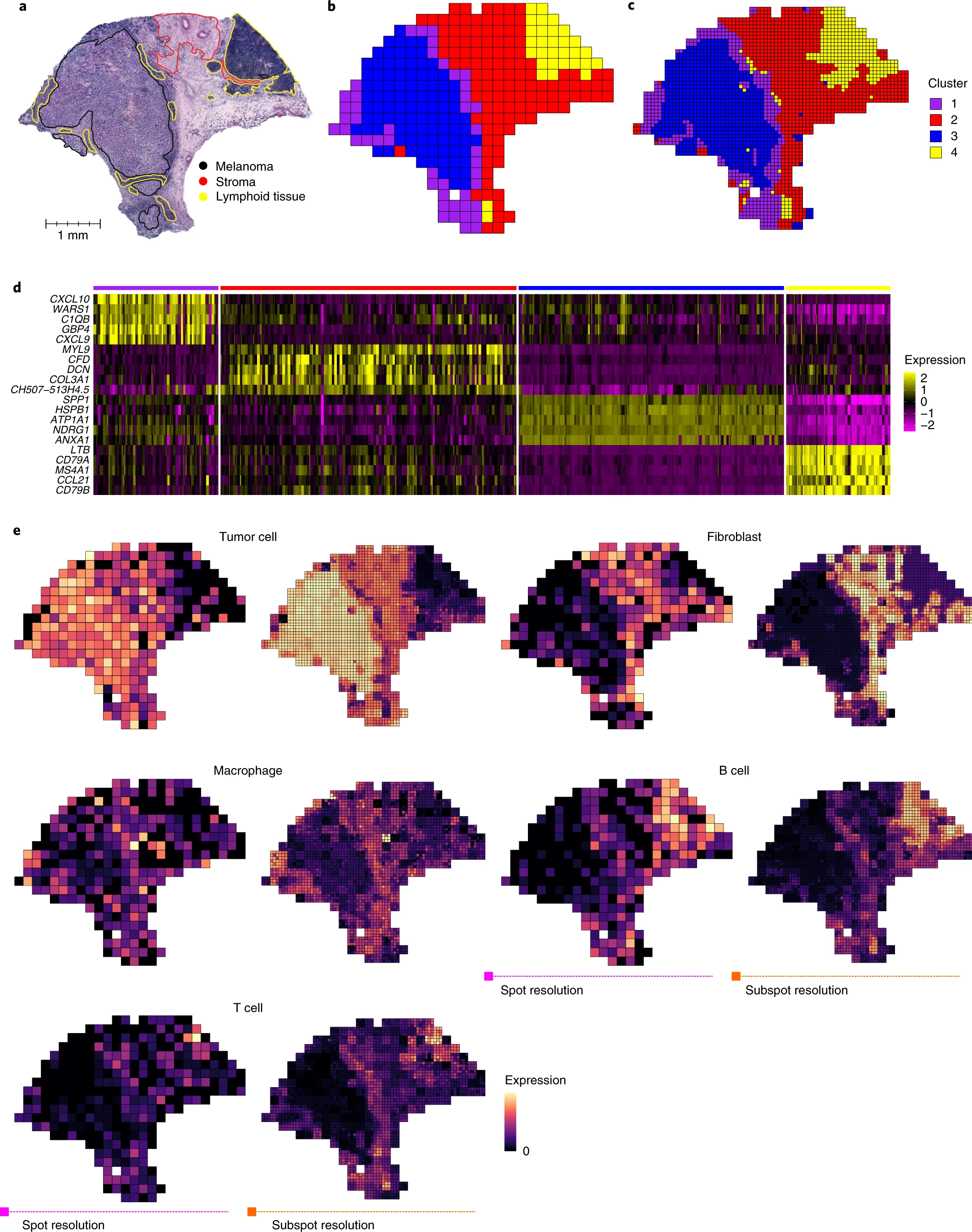
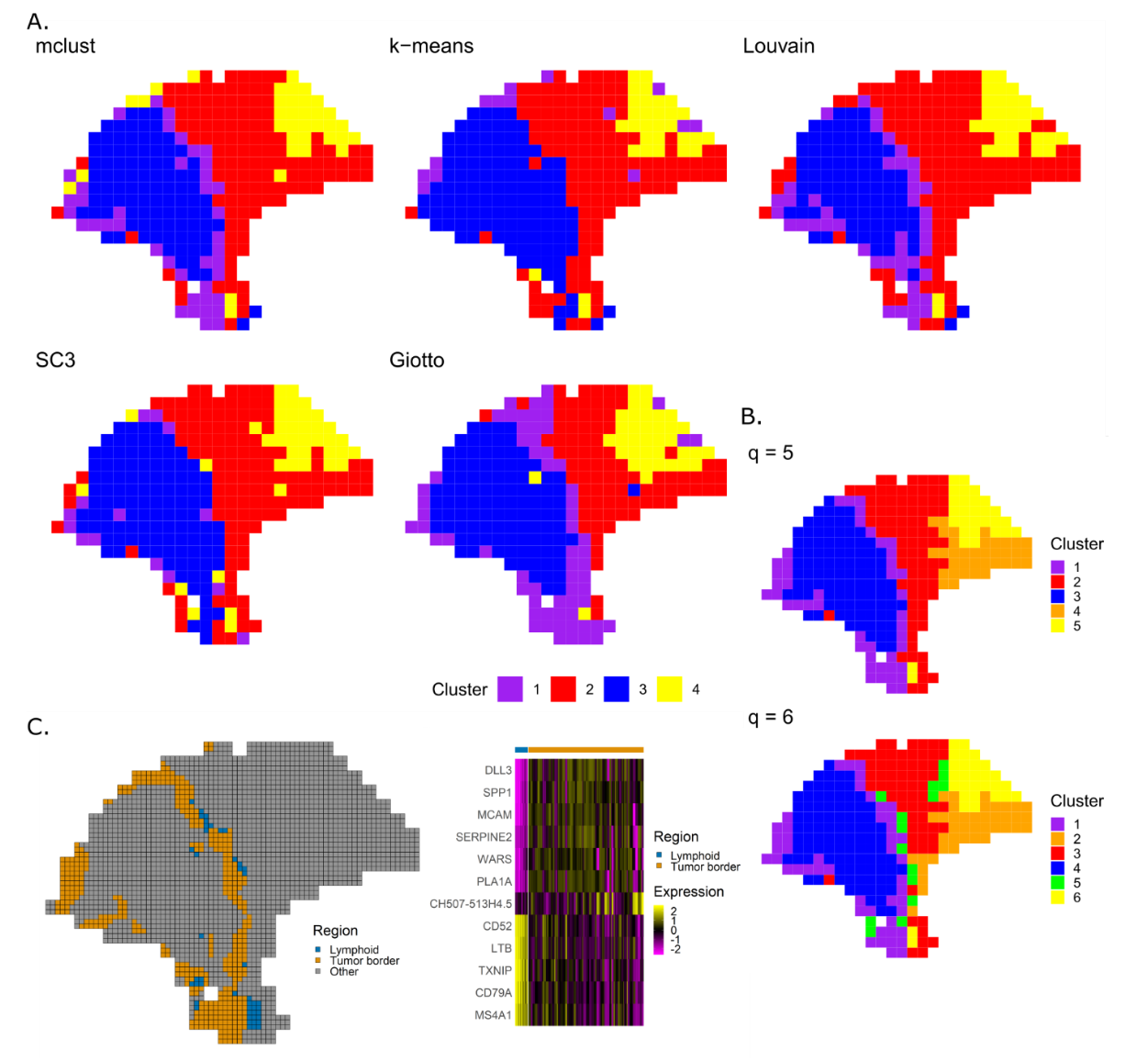
能够检测到淋巴细胞和肿瘤边界

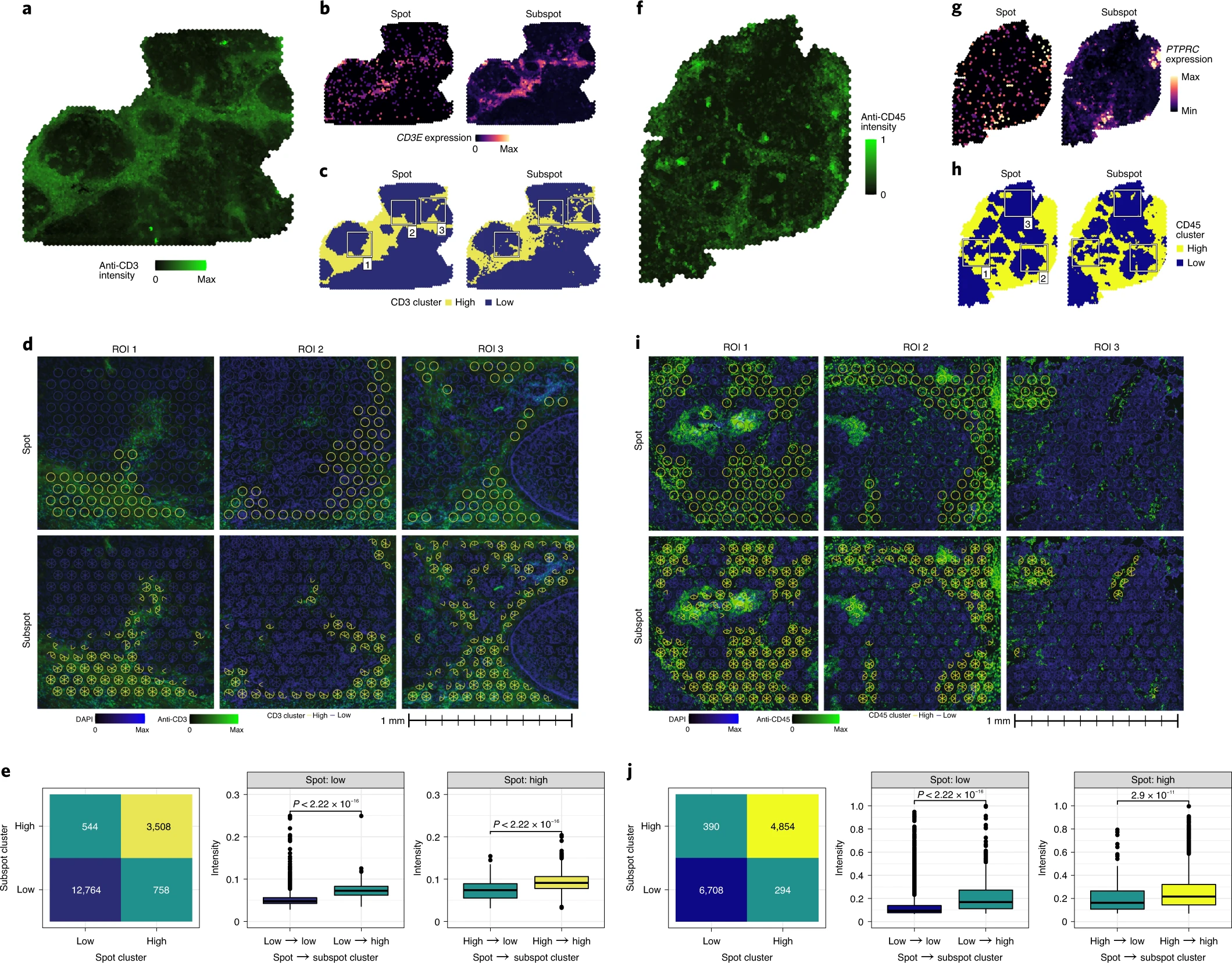
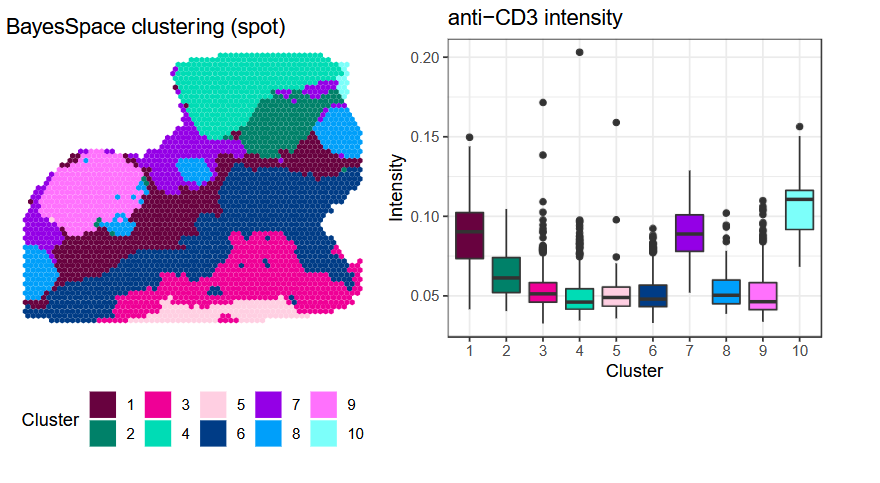
# Immunohistochemistry validates enhanced-resolution clusters

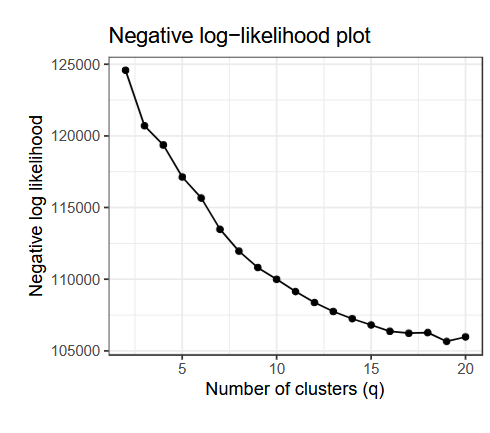
Negative Log-Likelihood Curve (负对数似然曲线) 是一种常用于评估模型性能或选择最佳参数的方法，尤其是在聚类分析中，它可以用于确定聚类数量（即分类簇数）。以下是关于它的详细介绍：

---

# 1. 什么是负对数似然 (Negative Log-Likelihood, NLL)?

• 似然函数（Likelihood Function）是统计模型中数据与参数匹配程度的度量，表示在给定参数下，观察到数据的概率。
  公式形式为：

  \begin{equation} L(\theta) = P(X | \theta) \end{equation}

  其中：

  • $X$ 是数据；
  • $\theta$ 是模型参数。

• 负对数似然：为了便于计算和优化，我们通常使用对数似然的负数：

  \begin{equation} \text{NLL} = - \log L(\theta) \end{equation}

  NLL 越小，表示模型越能够解释数据，参数 $\theta$ 越接近真实值。

---

# 2. 在聚类分析中的作用

在聚类问题中，NLL 可用于评估数据被分配到簇中的 “拟合质量”。常见方法包括基于混合模型的聚类（如高斯混合模型，GMM）：

• 混合模型聚类：
  在 GMM 中，我们假设数据来自多个正态分布（簇），每个簇由其均值和方差参数化。NLL 衡量模型的参数（包括簇数）对数据的解释能力。

• NLL 随簇数变化的趋势：

  • 如果簇数太少，模型的表达能力不足，NLL 会较高（模型不能很好地解释数据）。
  • 随着簇数增加，NLL 会逐渐减小，因为更多的簇能更细致地拟合数据。
  • 当簇数超过一定值后，NLL 的下降幅度减小，甚至趋于平稳（过拟合开始出现）。

这种趋势可以通过绘制 NLL 曲线来可视化。

---

# 3. 如何用 NLL 确定最佳簇数？

通过绘制 负对数似然曲线 (NLL Curve)，我们可以选择一个合理的聚类数量。以下是具体方法：

# 步骤：

1. 对于每个候选簇数 $k$（如 2 到 10 个簇）：
   • 训练模型（如 GMM）。
   • 计算对应的 NLL 值。
2. 绘制 NLL 曲线，横轴为簇数 $k$，纵轴为 NLL。

# 分析曲线：

• 曲线的 “肘点”（Elbow Point）：
  • 当 $k$ 增大时，NLL 减少的速度变慢。
  • 曲线的 “拐点” 对应的 $k$ 是一个合理的选择。
• 结合其他指标（如 BIC、AIC）验证，避免过拟合。

---

# 4. 与其他指标的关系

在确定聚类数量时，NLL 通常与其他模型选择指标配合使用：

• AIC（赤池信息准则）：

  \begin{equation} \text{AIC} = 2k - 2 \log L(\theta) \end{equation}

  $k$ 为参数数量，权衡拟合质量与模型复杂度。

• BIC（贝叶斯信息准则）：

  \begin{equation} \text{BIC} = k \log n - 2 \log L(\theta) \end{equation}

  $n$ 为样本数，更注重惩罚复杂模型。

# BayesSpace distinguishes intratumoral heterogeneity in IDC

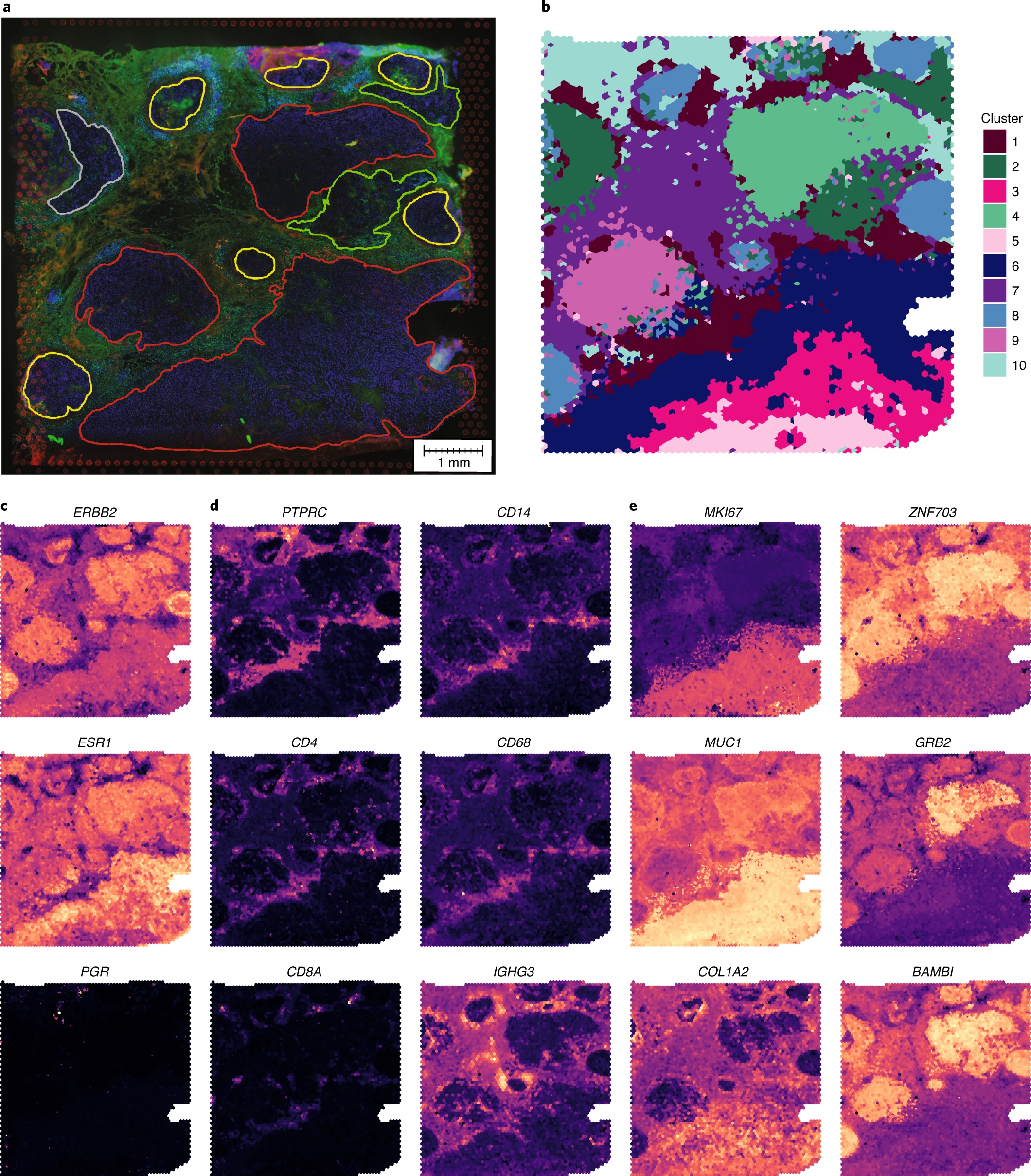
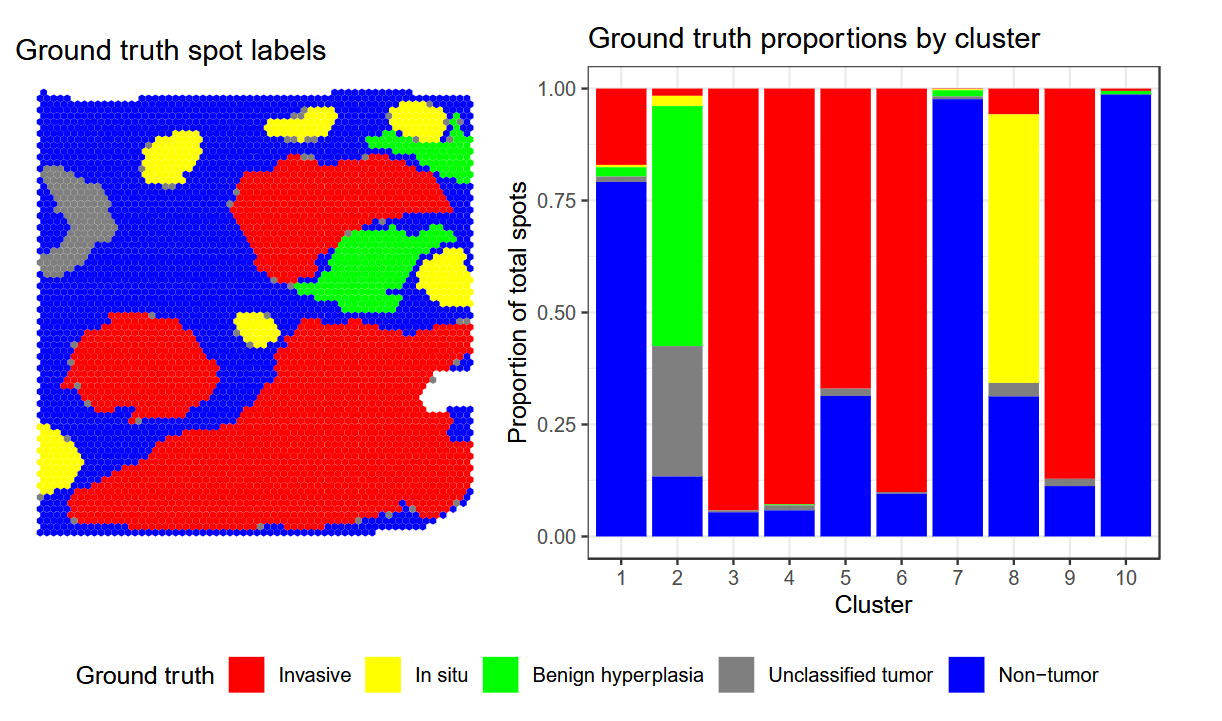
这里的聚类标签源自于这：

# BayesSpace enhances gene expression patterns to near single-cell resolution on in silico spatial data.

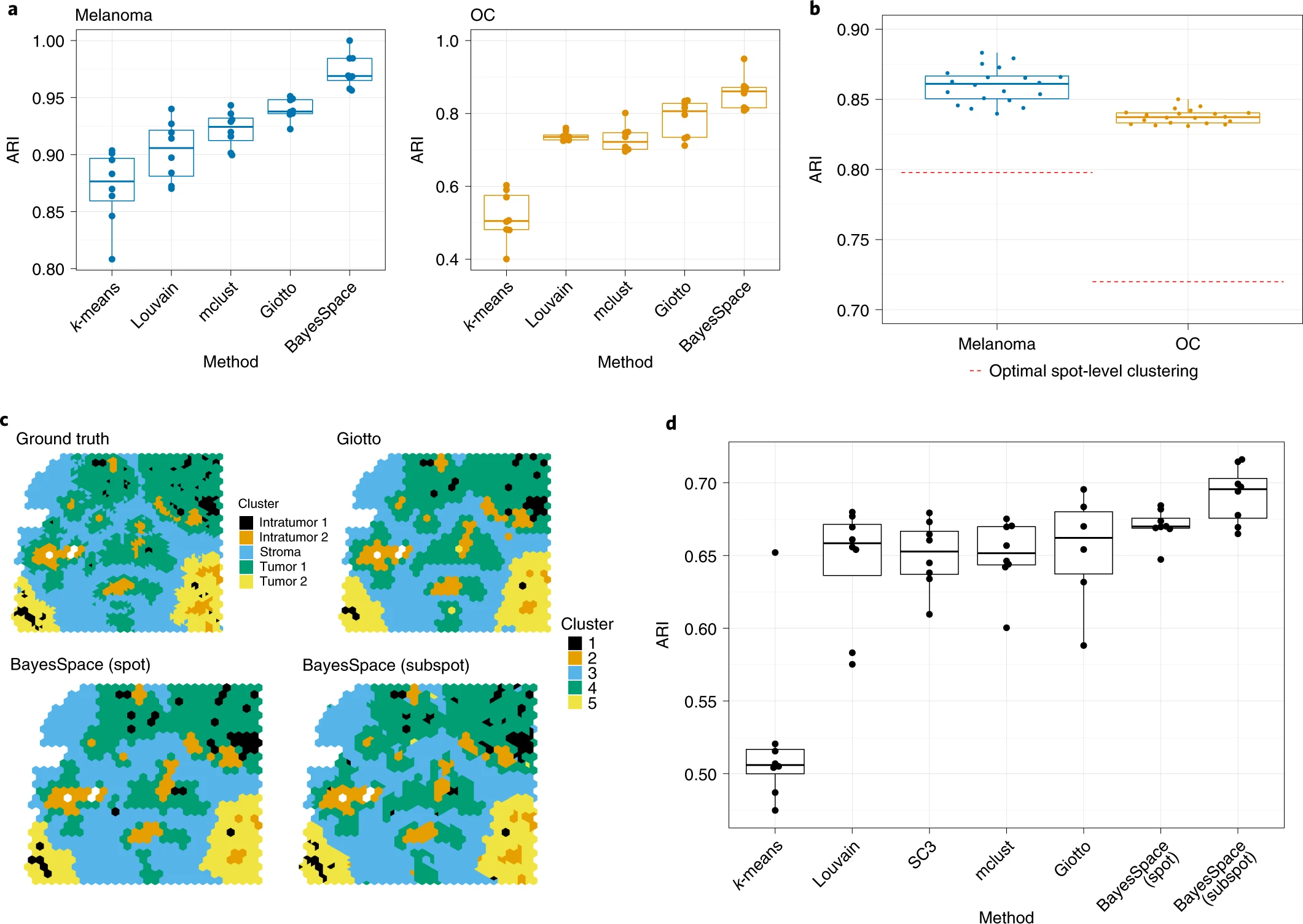
b 图：In N = 20 replicates for the simulation performed at the subspot level, BayesSpace enhanced clustering outperforms the optimal spot-level clustering (red dotted line)

# Enhanced-resolution clustering resolves keratinocyte structure in squamous cell carcinoma.

略

# Discussion

BayesSpace is a spatial transcriptomic model-based clustering method that uses a t-distributed error model to identify spatial clusters that are more robust to the presence of outliers caused bytechnical noise.

The resolution enhancement approaches single-cell resolution, with approximately three cells per subspot for data acquired with the Visium platform, without the need for external single-cell data.

However, there is potential for the enhanced data to be integrated with external single-cell data through deconvolution or label-transfer methods.

It may be possible to enhance the resolution of spot-level cell-type proportion estimates by using a Dirichlet regression model with enhanced PCs as predictors.

文章读下来感觉怪得很，后面恐怕需要再读几次。

# Methods

# Data description

# Preprocessing and dimension reduction

log transformed and normalized

PCA

# Spatial clustering model

We model the data as follows:

\begin{equation} (\gamma_i|z_i=k,w_i)\thicksim N(\gamma_i;\mu_k,w_i^{-1}\Lambda^{-1}) \end{equation}

For each spot $i$, a low $d$-dimensional representation $\gamma_i$ (for example, PCs) of the gene expression vector can be obtained.$z_i\in\{1,...,q\}$ denotes the latent cluster that $i$ belongs to, $\mu_k$ denotes the mean vector for cluster $k$, $\Lambda$ denotes the precision matrix, and $w_i$ denotes an unknown (observation-specific) scaling factor.

公式 $(\gamma_i \mid z_i = k, w_i) \sim N(\gamma_i; \mu_k, w_i^{-1} \Lambda^{-1})$ 出现在 BayesSpace 中，通常与空间转录组学数据的聚类或降维建模有关，涉及层次贝叶斯模型中的观测数据 $\gamma_i$、潜在分区 $z_i$、权重 $w_i$，以及高斯分布的参数化。

# 公式的含义逐步解释：

1. 条件分布：

   • $\gamma_i$：观测值（可能是一个维度的基因表达量向量或某些特征向量）。
   • $z_i$：潜在的分类标签，表示样本 $i$ 属于的簇 $k$。
   • $w_i$：权重变量，控制 $y_i$ 的方差大小，与样本 $i$ 的不确定性或尺度相关。

   给定 $z_i = k$ 和权重 $w_i$，$y_i$ 的分布是一个多元正态分布（multivariate normal distribution, $N$）。

2. 分布形式：

   • $N(\gamma_i; \mu_k, w_i^{-1} \Lambda^{-1})$ 表示 $y_i$ 服从一个均值为 $\mu_k$ 的多元高斯分布，协方差矩阵为 $(w_i^{-1} \Lambda^{-1})$。
     • $\mu_k$：簇 $k$ 对应的均值向量，表示属于该簇的样本的中心位置。
     • $\Lambda^{-1}$：基础协方差矩阵的逆，通常是一个固定的或学习得到的参数，控制簇的整体形状。
     • $w_i^{-1}$：权重 $w_i$ 的倒数，调整了协方差矩阵的大小。权重越大，协方差越小，样本 $i$ 的分布越集中；权重越小，分布越分散。

3. 解读：

   • 这个模型假设 每个样本的观测值 $y_i$ 的分布受制于其簇标签 $z_i = k$，并且协方差矩阵被权重 $w_i$ 调整：
     • 如果 $z_i = k$，那么样本 $i$ 更倾向于围绕簇中心 $\mu_k$ 分布。
     • $w_i^{-1}$ 调节了协方差，增加了个体样本的不确定性（允许不同样本对总体的贡献不同）。

# 相关背景理解：

• 层次贝叶斯模型：
  这种分布常见于 层次贝叶斯建模，其中通过潜在变量（如 $z_i$、$w_i$）引入柔性建模：

  • $z_i$ 定义了样本的类别分配。
  • $w_i$ 控制样本的不确定性或贡献。
    它们可以是模型推断的中间变量，也可能通过其他方式（如先验分布）进一步约束。

• 权重的作用：

  • 异方差性：允许不同样本具有不同的方差，增强了模型在处理异质性数据时的灵活性。
  • 在空间转录组学数据中，权重 $w_i$ 可以与空间相关性或技术误差相关，例如高噪声区域数据可能被赋予较小的权重。

# 总结：

公式表示：在给定样本属于簇 $k$（由 $z_i = k$ 指示）以及样本的权重 $w_i$ 的条件下，样本 $y_i$ 的分布是一个均值为 $\mu_k$、协方差为 $w_i^{-1} \Lambda^{-1}$ 的多元正态分布。权重 $w_i$ 用于刻画样本级别的异质性影响，$\Lambda$ 则控制簇级别的分布形状。

We also assume that the common precision matrix is unconstrained as there is correlation between PCs after conditioning on cluster,even though PCs are marginally uncorrelated

这里是说当考虑到簇的情况时，PCs 存在相关性。

The number of cluster $q$ is determined by prior boilogical knowledge when available or otherwise by the elbow of the pseudo-log-likelihood plot.We place the following priors on $\mu_k,\Lambda$ and $w_i$.

$$\begin{array}{c} \mu_k \overset{i.i.d}{\thicksim} N(\mu_0,\Lambda_0^{-1}) \\ \Lambda \overset{i.i.d}{\thicksim} Wishart_d(\alpha,diag(\beta)_d^{-1}) \\ w_i \overset{i.i.d}{\thicksim} \digamma(\frac{\nu}{2},\frac{\nu}{2}) \end{array}$$

i.i.d 是独立同分布的意思

这个公式描述了一个层次贝叶斯模型中参数的先验分布设定，广泛用于聚类、混合模型或者空间转录组学等场景，下面我逐步解释每个部分：

---

# 1. $\mu_k \overset{i.i.d}{\sim} N(\mu_0, \Lambda_0^{-1})$

• $\mu_k$：表示第 $k$ 个簇的均值向量。
• $N(\mu_0, \Lambda_0^{-1})$：表示均值的先验分布是一个多元正态分布，均值为 $\mu_0$，协方差矩阵为 $\Lambda_0^{-1}$。
  • $\mu_0$：是均值的中心，即所有簇的均值向量的中心。
  • $\Lambda_0$：是先验精度矩阵（精度矩阵是协方差矩阵的逆），用来控制簇均值的先验不确定性大小。
• 解释：
  • 这个假设表示每个簇的均值向量 $\mu_k$ 是在一个中心 $\mu_0$ 附近波动的，而波动的强弱由 $\Lambda_0^{-1}$ 控制。
  • 这种设置允许不同簇的均值在一个较为灵活的范围内变化。

---

# 2. $\Lambda \overset{i.i.d}{\sim} \mathrm{Wishart}_d(\alpha, \mathrm{diag}(\beta)_d^{-1})$

• $\Lambda$：表示精度矩阵（Precision Matrix），是协方差矩阵的逆矩阵。

• $\mathrm{Wishart}_d(\alpha, \mathrm{diag}(\beta)_d^{-1})$：表示精度矩阵的先验分布服从一个 $d$ - 维 Wishart 分布，其参数为：

  • $\alpha$：自由度参数，控制先验分布的集中程度。自由度越大，先验越集中。
  • $\mathrm{diag}(\beta)_d^{-1}$：尺度矩阵的逆。这里的 $\mathrm{diag}(\beta)$ 是一个对角矩阵，表示初始方差的尺度。

• 解释：

  • Wishart 分布是协方差矩阵（或精度矩阵）在贝叶斯框架中的自然共轭先验分布。
  • 这个假设表示精度矩阵 $\Lambda$ 是在一个对角结构附近波动的，通过自由度 $\alpha$ 和尺度矩阵 $\mathrm{diag}(\beta)$ 控制分布形状。
  • 由于 $\Lambda$ 影响数据的协方差，允许模型捕获簇内变量间的相关性。

---

# 3. $w_i \overset{i.i.d}{\sim} \digamma\left(\frac{\nu}{2}, \frac{\nu}{2}\right)$

• $w_i$：权重变量，通常控制样本 $i$ 的异方差性或不确定性。

• $\digamma\left(\frac{\nu}{2}, \frac{\nu}{2}\right)$：表示 $w_i$ 服从一个 Gamma 分布（或等价于一个逆卡方分布），其参数为：

  • 形状参数：$\frac{\nu}{2}$；
  • 率参数：$\frac{\nu}{2}$。

• 解释：

  • $w_i$ 的引入通常用于建模数据的权重异质性，即样本之间的方差不一定相同。
  • 这种 Gamma 分布（或等价的逆卡方分布）是异方差模型中的常见先验分布，适用于处理观测数据的噪声水平或权重不确定性。
  • $\nu$：自由度参数，控制 $w_i$ 的先验分布形状。较小的 $\nu$ 表示方差更大（权重更不确定），较大的 $\nu$ 表示权重更集中。

---

# 整体理解：

这组公式定义了一个层次贝叶斯模型中的参数先验分布：

1. $\mu_k$：描述簇 $k$ 的中心均值，先验为一个多元正态分布。
2. $\Lambda$：描述簇 $k$ 的协方差（或精度矩阵），先验为 Wishart 分布，允许簇内变量存在相关性。
3. $w_i$：为每个样本引入权重或方差的不确定性，先验服从 Gamma 分布，适应数据的异方差性。

这样的模型可以灵活捕获：

• 簇间均值的变动（通过 $\mu_k$）。
• 簇内变量的相关性结构（通过 $\Lambda$）。
• 样本级别的方差差异（通过 $w_i$）。

这些先验设定的选择使得模型在面对高维数据时具有良好的表达能力和鲁棒性，非常适合用于聚类、空间数据建模等场景。

By default, we set $\mu_0$ to be the the empirical mean vector of the data, which is generally the zero vector for PCA input.

$\Lambda_0$ is set to 0.01 times the identity matrix to provide a weak prior that will be dominated by the data when there are spots assigned to the cluster.Similarly, we set $\alpha=1$ and $\beta =0.01$ to provide a weak prior for the precision matrix. $\nu$ denotes a fixed degrees-of-freedom parameter to control the heaviness of tails and was set to $\nu=4$, which was previously shown to overcome the influence of outlier spots during clustering.

We also assume that $\gamma_i$ and $w_i$ are independent. As such, when marginalizing over $w_i$, our normal likelihood becomes a multivariable $t$ distribution with a mean of 0 and convariance matrix \frac{\nu}{\nu -2}\Lambda^

这句话的核心涉及多变量 t 分布的形成，以及对 $w_i$ 进行边际化（Marginalization）操作的结果。下面详细解析：

---

# 1. 背景：$w_i$ 和 $\gamma_i$ 独立假设

• $\gamma_i$ 代表某个随机变量或潜在因子。
• $w_i$ 是一个权重参数（通常用于引入异方差或模型的权重不确定性）。
• 假设 $w_i$ 和 $\gamma_i$ 独立，意味着：
  • 它们之间没有统计相关性。
  • 这种独立性使得在计算边际分布时，可以将它们的联合分布进行分解。

---

# 2. 正态分布与 $w_i$ 的引入

我们最初的模型假设：

$$\begin{array}{c} y_i \mid \gamma_i, w_i \sim N(0, w_i^{-1} \Lambda^{-1}) \end{array}$$

这里：

• $w_i$ 是一个缩放参数，它与精度（precision）有关，$w_i^{-1}$ 表示对精度的缩放。
• $\Lambda$ 是一个精度矩阵（协方差矩阵的逆）。

解释：

• 若 $w_i$ 是确定的，$y_i$ 服从均值为 0，精度矩阵为 $w_i \Lambda$ 的多变量正态分布。

但是，如果我们将 $w_i$ 视为随机变量，并对其进行边际化（即不再固定 $w_i$ 的取值，而是将它的分布也考虑进来），则结果不再是正态分布，而是多变量 t 分布。

---

# 3. 边际化 $w_i$：从正态分布到 t 分布

• 假设 $w_i \sim \text{Gamma}(\frac{\nu}{2}, \frac{\nu}{2})$（伽马分布的形式）。
• 由于 $w_i$ 是精度的缩放因子，它的引入会导致边际分布的重尾特性（更大的方差，尾部概率更高）。

通过将 $w_i$ 在似然函数中积分掉（即边际化），结果会导致原始正态分布转变为多变量 t 分布。

---

# 4. 多变量 t 分布的参数解释

当边际化 $w_i$ 后，$\gamma_i$ 的分布变为：

$$\begin{array}{c} \gamma_i \sim t_\nu(0, \Sigma) \end{array}$$

其中：

• $t_\nu$：自由度为 $\nu$ 的多变量 t 分布。
• 均值：$0$（原始正态分布的均值）。
• 协方差矩阵：$$\beginarray}{c} \Sigma = \frac{\nu}{\nu - 2} \Lambda({-1)
  \end{array}$$

# 为何出现 $\frac{\nu}{\nu - 2}$？

1. 由于 $w_i$ 的分布为 Gamma 分布，其自由度参数为 $\nu$。
2. $w_i$ 的边际化操作会引入一个缩放因子，导致协方差矩阵被调整为 $\frac{\nu}{\nu - 2}\Lambda^{-1}$。
   • 这里的 $\frac{\nu}{\nu - 2}$ 是一个尺度因子，它反映了 t 分布的方差膨胀，因为 t 分布具有重尾特性，相比正态分布方差更大。

# 自由度 $\nu$ 的影响：

• 当 $\nu \to \infty$ 时，$\frac{\nu}{\nu - 2} \to 1$，t 分布会逐渐收敛为正态分布。
• 当 $\nu$ 较小（比如 $\nu = 3, 4$）时，t 分布具有更重的尾部。

---

# 5. 直观理解

• $w_i$ 的引入导致样本点的方差具有不确定性（异方差性）。
• 对 $w_i$ 进行边际化相当于将这种方差的不确定性融入到分布中，结果使得分布变得重尾，从而形成了 t 分布。
• t 分布的方差由 $\Lambda^{-1}$ 决定，但它被因子 $\frac{\nu}{\nu - 2}$ 膨胀，从而体现了重尾特性。

---

# 总结

这句话说明了由于对 $w_i$ 进行边际化，原本的正态分布变成了多变量 t 分布。

• t 分布的重尾特性源于 $w_i$ 的随机性，它使得异常值（Outliers）更可能出现。
• 协方差矩阵 $\frac{\nu}{\nu - 2}\Lambda^{-1}$ 反映了这种分布的方差膨胀效应，其中 $\nu$ 控制尾部的厚度。

边际化（Marginalization）是概率论中的一种常见技术，指的是从联合分布中 “去除” 某些变量，得到剩余变量的边际分布。具体来说，就是对某些变量进行积分或求和，消去这些变量的影响，从而得到其他变量的概率分布。

# 边际化的基本概念

假设我们有一组随机变量 $X = (X_1, X_2, \dots, X_n)$，它们的联合分布是 $p(X_1, X_2, \dots, X_n)$，那么边际化就是求去掉某些变量后，其他变量的边际分布。具体的操作是对要去除的变量进行积分（或求和）。

例如，若我们想得到 $X_1$ 的边际分布，可以通过以下方式进行边际化：

$$\begin{array}{c} p(X_1) = \int p(X_1, X_2, \dots, X_n) \, dX_2 \, dX_3 \, \dots \, dX_n \end{array}$$

这表示我们对除了 $X_1$ 之外的所有变量进行积分，从而得到了 $X_1$ 的边际分布。换句话说，边际化操作通过 “去除” 其他变量，计算出一个变量的整体分布。

# 边际化在贝叶斯推断中的应用

在贝叶斯推断中，边际化经常用于消除隐变量或不关注的参数的影响，从而得到感兴趣的变量的后验分布。

举个例子，假设我们有一个含有参数 $w_i$ 和 $y_i$ 的联合分布模型，模型的形式是：

$$\begin{array}{c} p(y_i, w_i \mid \theta) = p(y_i \mid w_i, \theta) p(w_i \mid \theta) \end{array}$$

如果我们不关心 $w_i$，而只对 $y_i$ 的分布感兴趣，我们就需要边际化 $w_i$：

$$\begin{array}{c} p(y_i \mid \theta) = \int p(y_i \mid w_i, \theta) p(w_i \mid \theta) \, dw_i \end{array}$$

在这种情况下，边际化操作去除了 $w_i$ 变量，只保留了 $y_i$ 的边际分布。

# 边际化的作用

边际化常常有助于简化模型并使得计算更加可行，尤其是当涉及到复杂的联合分布时。通过边际化，我们可以消除模型中的一些冗余或不必要的变量，专注于感兴趣的部分。

# 在 t 分布的例子中

在你提到的 t 分布的例子中，边际化是指将 $w_i$ （它是一个随机变量，控制着方差或精度）从联合分布中去除。原始的似然函数假设了一个正态分布，但是因为 $w_i$ 是随机的，我们需要将它在其可能的值上进行积分（边际化），从而得到一个新的分布，这个新的分布变成了一个多变量 t 分布。

This formulation allows us to use a simple Gibbs sampling for updating most of the parameters because the observations are normally distributed when conditioning on $w_i$.

Gibbs Sampling 是一种马尔科夫链蒙特卡罗（MCMC）方法，用于从复杂的多维分布中生成样本，特别适用于无法直接采样的高维概率分布。其核心思想是通过反复条件采样（conditional sampling）来模拟联合分布中的各个变量。

# 基本思想

Gibbs Sampling 的基本思想是：给定一个多维分布 $p(x_1, x_2, \dots, x_n)$，我们通过依次从每个变量的条件分布中采样，逐步更新所有变量，最终得到该联合分布的样本。

对于一个多维随机变量 $X = (x_1, x_2, \dots, x_n)$，其联合分布为 $p(x_1, x_2, \dots, x_n)$，我们依次从条件分布中采样：

1. 从条件分布 $p(x_1 \mid x_2, x_3, \dots, x_n)$ 中采样得到新的 $x_1$。
2. 从条件分布 $p(x_2 \mid x_1, x_3, \dots, x_n)$ 中采样得到新的 $x_2$。
3. 重复这个过程，直到所有变量都被更新一次。

然后，这些采样值形成了一个样本，代表了联合分布的一个近似。通过多次迭代，可以得到一个收敛到目标联合分布的样本序列。

# Gibbs Sampling 的步骤

假设我们有一个包含 $n$ 个随机变量的联合分布 $p(x_1, x_2, \dots, x_n)$，Gibbs 采样的步骤如下：

1. 初始化：给定一个初始值 $x_1^{(0)}, x_2^{(0)}, \dots, x_n^{(0)}$。
2. 迭代：对于每次迭代 $t$，依次更新每个变量：
   • $x_1^{(t)} \sim p(x_1 \mid x_2^{(t-1)}, x_3^{(t-1)}, \dots, x_n^{(t-1)})$
   • $x_2^{(t)} \sim p(x_2 \mid x_1^{(t)}, x_3^{(t-1)}, \dots, x_n^{(t-1)})$
   • 依此类推，直到更新所有变量。
3. 收集样本：每次迭代完成后，保存新的样本 $(x_1^{(t)}, x_2^{(t)}, \dots, x_n^{(t)})$。

# 条件分布

Gibbs Sampling 之所以有效，是因为它依赖于能够从条件分布中采样，而不需要知道联合分布的具体形式。如果每个变量的条件分布 $p(x_i \mid x_1, \dots, x_{i-1}, x_{i+1}, \dots, x_n)$ 可以计算出来并且易于采样，那么 Gibbs Sampling 就能有效地从联合分布中抽取样本。

# 收敛性

• 在 Gibb 采样中，随着迭代的进行，生成的样本逐渐收敛到目标联合分布。通常，我们通过 "burn-in" 期来丢弃前几轮迭代的样本，以确保样本已经接近目标分布。
• 在进行充分的迭代后，生成的样本可以被视为目标联合分布的近似。

# 应用场景

Gibbs Sampling 被广泛应用于以下领域：

• 贝叶斯推断：在贝叶斯模型中，常常需要计算后验分布，Gibbs Sampling 可以用于从后验分布中采样。
• 隐马尔可夫模型（HMM）：在 HMM 中，隐藏的状态序列可以通过 Gibbs Sampling 来采样。
• 图模型：在概率图模型中，通过 Gibbs Sampling 可以从联合分布中抽样。

# 优点

• 简单易实现：每次只需要从一个变量的条件分布中采样，因此非常直观和容易实现。
• 适用于高维问题：对于高维数据，Gibbs Sampling 仍然适用，因为它将高维问题分解成多个低维条件分布的问题。
• 不需要计算整体分布：只需要计算每个变量的条件分布，而不需要计算联合分布的全貌。

# 缺点

• 依赖条件分布：如果某些条件分布很难采样，Gibbs Sampling 就可能变得非常低效或不可行。
• 收敛性问题：在某些情况下，Gibbs Sampling 可能收敛很慢，尤其是在目标分布中存在强相关性的情况下。
• 局部最优：如果初始值选择不当，Gibbs Sampling 可能陷入局部最优解，导致采样效果不好。

# 总结

Gibbs Sampling 是一种强大的 MCMC 方法，通过循环更新每个变量的条件分布，逐步生成联合分布的样本。它适用于许多需要从复杂分布中采样的贝叶斯推断问题，尤其是当目标分布的条件分布容易采样时。

这句话的意思是：由于当条件化于 $w_i$ 时，观测数据（即 $\gamma_i$）呈正态分布，因此可以使用简单的 Gibbs 采样 来更新大多数参数。

# 详细解析：

1. $\gamma_i \sim t_\nu(0, \Sigma)$：
   这表示 $\gamma_i$ 服从自由度为 $\nu$ 的 t 分布，均值为 0，协方差矩阵为 $\Sigma$。在 Gibbs 采样中，我们关心的是在给定其他条件（如 $w_i$）下，如何进行采样。

2. “当条件化于 $w_i$ 时，观测数据呈正态分布”：
   这句话的意思是，给定 $w_i$ 的值后，$\gamma_i$ 的分布变成了正态分布。也就是说，$\gamma_i$ 可能在条件分布下具有 t 分布，但一旦知道了 $w_i$，$\gamma_i$ 的分布就变成了正态分布。

   • 这是因为 t 分布可以看作是一个正态分布和一个伽马分布（精度分布）的混合，边际化掉伽马分布后，得到的条件分布通常会是正态分布。

3. “使用简单的 Gibbs 采样来更新大多数参数”：

   • 在 Gibbs 采样中，通常我们需要从每个参数的条件分布中采样。如果某个参数的条件分布是已知的且容易采样，那么可以使用简单的 Gibbs 采样更新该参数。
   • 在这里，条件分布是指在给定 $w_i$ 的情况下，$\gamma_i$ 的分布变为正态分布，且此正态分布的均值和方差（或协方差矩阵）是可以计算的。
   • 因为正态分布的条件分布是已知的（即每个变量在给定其他变量的条件下是正态分布），所以 Gibbs 采样可以很方便地进行，从而更新模型中的其他参数。

# 简化的关键

• 条件正态分布：在 Gibbs 采样中，每个参数的条件分布需要是简单的，特别是正态分布的形式。因为正态分布的采样非常直接且高效，不需要复杂的计算。

• 边际化和简化：虽然 $\gamma_i$ 服从 t 分布，但当我们条件化于 $w_i$ 后，它变为正态分布，这大大简化了采样过程。

• Gibbs 采样的优势：Gibbs 采样依赖于条件分布的简单性。如果某个变量的条件分布是正态分布，则从中采样非常直接，更新过程也变得简单。因此，使用 Gibbs 采样时，模型中的其他参数（如 $w_i$）的更新可以通过简单的条件正态分布来进行。

# 总结

这句话的意思是：在模型中，$\gamma_i$ 的条件分布（在给定 $w_i$ 的情况下）是正态分布，这使得我们能够利用 Gibbs 采样 方便地更新其他参数。由于条件正态分布的性质，我们可以通过简单的采样步骤来更新大多数模型参数，从而加速了模型的推断过程。

$w_i$ values can also be interpreted as weights; the model will simply estimate a small weight value for any potential outlying data value.This provides robustness against outliers that can be commonly encountered in these types of data.

这一步将可能出现的突出的数据给放小，加强了数据的鲁棒性。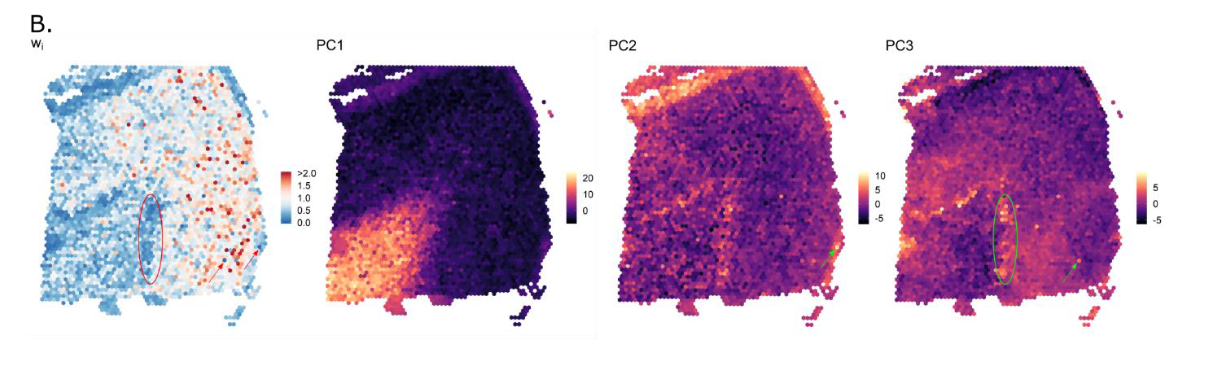

上图是 The spatial distribution of $w_i$'s is shown for sample 151673. 可以看到许多可见的在 PC2 和 PC3 的突出点被 downweighted 了。

Estimation of parameters is carried out using an MCMC method.

We intialize $\textbf{z}$ using a non-spatial clustering method such as mclust by default.

Alternative initializations can also be supplied as a label vector. Next, iteratively and sequentially, each $\mu_k$,$\Lambda$ and $w_i$ is updated via Gibbs sampling, and each $z_i$ is updated via the Metropolis-Hasting algorithm.

Metropolis-Hastings 算法是一个经典的 MCMC（马尔科夫链蒙特卡罗） 采样算法，用于从复杂的概率分布中生成样本。该算法的核心思想是利用一个马尔科夫链，通过构造一个提议分布来生成候选样本，并根据某种接受规则决定是否接受这些样本。最终，这个链会收敛到目标分布，从而允许我们从目标分布中进行采样。

# Metropolis-Hastings 算法的步骤

假设我们想从目标分布 $\pi(x)$ 中生成样本。Metropolis-Hastings 算法的基本步骤如下：

1. 初始化：
   选择初始状态 $x_0$，即初始样本。

2. 迭代过程：

   • 对于每一轮迭代 $t$（$t = 1, 2, 3, \dots$）：

     • 提议分布：从当前样本 $x_t$ 根据某个提议分布 $q(x' | x_t)$ 生成一个新的候选样本 $x'$。这个提议分布可以是对称的（如正态分布）或不对称的（如从不同的分布中提取）。

     • 计算接受概率：计算接受概率 $\alpha(x_t, x')$，即候选样本 $x'$ 被接受的概率，通常定义为：

       $$\begin{array}{c} \alpha(x_t, x') = \min\left(1, \frac{\pi(x') q(x_t | x')}{\pi(x_t) q(x' | x_t)}\right) \end{array}$$

       其中：

       • $\pi(x')$ 是候选样本 $x'$ 在目标分布中的概率密度。
       • $\pi(x_t)$ 是当前样本 $x_t$ 在目标分布中的概率密度。
       • $q(x_t | x')$ 和 $q(x' | x_t)$ 分别是提议分布从 $x'$ 到 $x_t$ 和从 $x_t$ 到 $x'$ 的转移概率。

     • 接受或拒绝：

       • 生成一个均匀分布的随机数 $u \sim U(0, 1)$。
       • 如果 $u \leq \alpha(x_t, x')$，则接受候选样本 $x'$ 作为新的样本 $x_{t+1} = x'$。
       • 否则，拒绝候选样本，保持当前样本 $x_{t+1} = x_t$。

3. 重复迭代：
   重复上述过程，直到达到足够多的样本。随着迭代次数的增加，样本将趋近于目标分布 $\pi(x)$。

# 接受概率的解释

接受概率 $\alpha(x_t, x')$ 的形式确保了当提议样本 $x'$ 来自目标分布时，样本是平衡的。如果提议样本 $x'$ 比当前样本 $x_t$ 更符合目标分布（即 $\pi(x') > \pi(x_t)$），则总是接受 $x'$。如果 $x'$ 不太符合目标分布，则按一个概率来接受它，这有助于避免采样过程陷入局部最优。

# Metropolis-Hastings 算法的特点

• 目标分布不需要归一化常数：Metropolis-Hastings 算法可以用于无法直接计算或复杂的目标分布，因为它不需要知道目标分布的归一化常数（即 $\pi(x)$ 中的常数部分）。只要目标分布的形状是已知的，算法就能工作。

• 提议分布的灵活性：提议分布 $q(x' | x_t)$ 可以是任何合理的分布。通常，选择对称的提议分布（如正态分布）可以简化算法，但也可以选择不对称的分布来提高采样效率。

• 收敛性：尽管 Metropolis-Hastings 算法能有效地从目标分布中采样，但收敛速度可能较慢，特别是在高维空间或复杂的目标分布下。为了解决这个问题，通常需要进行多次迭代并适当调整提议分布。

# 举例：从标准正态分布中采样

假设我们希望从标准正态分布 $\mathcal{N}(0, 1)$ 中采样。我们可以使用 Metropolis-Hastings 算法，选择一个对称的提议分布（比如 $q(x' | x_t) = \mathcal{N}(x_t, \sigma^2)$，即从当前样本 $x_t$ 出发，根据正态分布生成候选样本）。

1. 初始化 $x_0 = 0$。
2. 在每次迭代中，从 $x_t$ 生成一个候选样本 $x' \sim \mathcal{N}(x_t, \sigma^2)$。
3. 计算接受概率：

   $$\begin{array}{c} \alpha(x_t, x') = \min\left(1, \frac{\mathcal{N}(x')}{\mathcal{N}(x_t)}\right) = 1 \quad \text{(因为目标分布是对称的)}. \end{array}$$

4. 使用接受概率决定是否接受 $x'$ 作为新的样本。

# 总结

Metropolis-Hastings 算法是一种广泛使用的 MCMC 方法，用于从复杂的目标分布中生成样本。通过构建一个马尔科夫链并根据提议分布生成候选样本，再根据接受概率决定是否接受这些样本，最终得到的样本将趋近于目标分布。该方法具有灵活性，可以处理目标分布不完全已知的情况，但收敛速度可能较慢，尤其是在高维空间中。

Specifically, each $z_i$ is updated by taking into account both the likelihood and spatial prior information. The Markov random foeld prior is given by the Potts model:

\begin{equation} \pi(z_i)=exp(\frac{\delta}{|\langle ij\rangle|}\times \sum_{\langle ij\rangle}I(z_i=z_j)) \end{equation}

where $\langle ij\rangle$ denotes all spots $j$ that are neighbors of $i$, $I$ represents the indicator function, and $\delta$ is a fixed parameter controlling the strength of the smoothing.In this way, neighboring spots are encouraged to belong to the same cluster.

你提到的这个公式是 Potts 模型的先验（prior）分布，通常用于马尔科夫随机场（Markov Random Field, MRF）中。它通过一种特殊的方式编码了邻域之间的相似性，特别适用于图像、标记、聚类等任务。

我们可以逐步解析这个公式：

# Potts 模型的先验分布：

$$\begin{array}{c} \pi(z_i) = \exp\left( \frac{\delta}{|\langle ij \rangle|} \times \sum_{\langle ij \rangle} I(z_i = z_j) \right) \end{array}$$

# 1. Potts 模型的基本思想

Potts 模型通常用于马尔科夫随机场中，用于描述一个节点（例如一个像素、标签或其他离散变量）与其邻域的相似性。它的核心思想是相邻节点的标签倾向于相同，即相邻的 (z_i) 和 (z_j) 值越相同，模型的概率越大。

# 2. 公式的组成部分

• $z_i$：这是节点 (i) 上的随机变量，可能代表标签、类别或状态。

• $\langle ij \rangle$：表示一对相邻节点 (i) 和 (j)，例如在图像中相邻的像素点，或者在图聚类中的相邻簇。

• $|\langle ij \rangle|$：表示相邻节点对的总数。这个数值通常与邻接关系的数量有关，比如在图像处理中，每个像素的邻居数量。

• $\sum_{\langle ij \rangle} I(z_i = z_j)$：这是一个求和项，对所有相邻节点对进行求和。当 $z_i = z_j$ 时，$I(z_i = z_j) = 1$（即两个相邻节点标签相同），否则为 0。

• $\delta$：是一个正的常数，用于控制相邻节点标签相同的影响程度。较大的 $\delta$ 会增强相邻节点标签相同的倾向。

# 3. 解读 Potts 模型的先验分布

• 相邻节点的标签相同的偏好：这个模型的核心是，邻居 (i) 和 (j) 如果有相同的标签（即 $z_i = z_j$），则对整体模型的概率有正面贡献。具体来说，这个贡献是通过指示函数 $I(z_i = z_j)$ 来实现的。如果两个相邻的 (z_i) 和 (z_j) 相同，则增加该项的和，从而增加 Potts 模型的概率。

• 概率的形式：这个先验分布是指数形式，意味着我们希望相邻节点有相同标签时，模型的概率较高。分布越大，表示相邻节点的标签相同的 “倾向” 越强。这个先验模型是通过指数函数来控制相邻节点标签相同的影响强度。

• 参数 $\delta$：参数 $\delta$ 控制着这个相似性强度。如果 $\delta$ 较大，则表示节点之间相似的偏好较强，倾向于让相邻节点有相同标签；如果 $\delta$ 较小，则相邻节点标签相同的偏好较弱。

• $\frac{1}{|\langle ij \rangle|}$：这个因子是归一化因子，确保 Potts 模型的计算能够考虑所有相邻节点对的贡献。它的作用是让模型对每个相邻对的贡献进行平衡。

在 Metropolis-Hastings 算法中结合 Potts 模型的先验（即 (\pi (z_i))）的步骤可以分为以下几个部分。通过这些步骤，Metropolis-Hastings 算法更新节点标签（(z_i)）时，会根据 Potts 模型的相邻节点标签相同的偏好，决定是否接受一个新的标签配置。

# Metropolis-Hastings 更新步骤与 Potts 模型结合

假设我们的目标是更新节点 $z_i$（例如图像中的一个像素、聚类中的一个样本等），我们将结合目标分布（通常是数据的似然）和 Potts 模型的先验，进行以下步骤：

# 1. 初始化

假设你已经有了当前的状态 $\{z_1, z_2, \dots, z_n\}$（所有节点的标签），并且你希望更新某个节点 $z_i$ 的标签。

# 2. 提议分布

• 生成候选标签：根据某种提议分布，生成节点 $z_i$ 的新标签 $z_i'$。这个提议分布通常是从一个固定的离散集合中选择（例如，如果 $z_i$ 是一个分类标签，则提议分布可能是在所有类别中均匀选择，或者基于某些启发式方法选择）。

# 3. 计算接受概率

• 目标分布（Posterior）：目标分布通常由数据的似然和先验分布组成。假设数据的似然是 $p(\text{data} | \{z_i\})$，那么整个后验分布就是：

  $$\begin{array}{c} p(\{z_i\} | \text{data}) \propto p(\text{data} | \{z_i\}) \cdot \pi(\{z_i\}) \end{array}$$

  其中，(\pi ({z_i})) 是根据 Potts 模型给出的先验分布，表示相邻节点标签相同的偏好。

• 计算 Potts 模型的先验分布：首先，根据 Potts 模型的公式计算当前标签配置 $\{z_1, z_2, \dots, z_n\}$ 的先验概率：

  $$\begin{array}{c} \pi(\{z_i\}) = \prod_{\langle ij \rangle} \exp\left( \frac{\delta}{|\langle ij \rangle|} I(z_i = z_j) \right) \end{array}$$

  其中，$\langle ij \rangle$ 是所有相邻节点对， $I(z_i = z_j)$ 是指示函数，若 (z_i = z_j)，则 (I (z_i = z_j) = 1)，否则为 0。

• 候选配置的先验：然后，计算候选标签 $z_i'$ 的先验概率 $\pi'(\{z_i'\})$，类似于上面计算 $\pi(\{z_i\})$ 的方式：

  $$\begin{array}{c} \pi'(\{z_i'\}) = \prod_{\langle ij \rangle} \exp\left( \frac{\delta}{|\langle ij \rangle|} I(z_i' = z_j) \right) \end{array}$$

• 接受概率：在 Metropolis-Hastings 算法中，接受概率 $\alpha$ 是基于当前状态和候选状态的目标分布之比来计算的。由于目标分布是先验和似然的乘积，接受概率 $\alpha(z_i, z_i')$ 的计算公式为：

  $$\begin{array}{c} \alpha(z_i, z_i') = \min\left( 1, \frac{p(\text{data} | z_1, z_2, \dots, z_n, z_i') \cdot \pi'(\{z_i'\})}{p(\text{data} | z_1, z_2, \dots, z_n, z_i) \cdot \pi(\{z_i\})} \right) \end{array}$$

  其中：

  • $p(\text{data} | z_1, z_2, \dots, z_n, z_i)$ 和 $p(\text{data} | z_1, z_2, \dots, z_n, z_i')$ 是数据的似然，通常与数据和当前标签（或候选标签）之间的匹配程度相关。
  • $\pi(\{z_i\})$ 和 $\pi'(\{z_i'\})$ 分别是当前标签配置和候选标签配置的 Potts 模型先验。

# 4. 接受或拒绝

• 生成一个均匀分布的随机数 $u \sim U(0, 1)$。
• 如果 $u \leq \alpha(z_i, z_i')$，则接受候选标签 $z_i'$ 作为新的标签 $z_i = z_i'$。
• 否则，保持原标签 $z_i$。

# 5. 重复更新

• 重复上述步骤，直到更新整个标签集，或者直到满足收敛条件。

# 为什么选择 Metropolis-Hastings 更新 Potts 模型？

• 相邻标签的相似性：Potts 模型的先验确保相邻节点具有相同标签的倾向，Metropolis-Hastings 通过在每次更新时利用这个先验，控制了标签之间的相似性。

• 高效的更新：通过结合数据的似然和 Potts 模型的先验，Metropolis-Hastings 算法能够有效地进行标签更新，逐渐收敛到一个标签配置，其中相邻标签相似且与数据匹配。

# 总结

• Potts 模型的先验：通过指数函数形式使得相邻节点具有相同标签的可能性更大，适用于马尔科夫随机场中的标签平滑。

• Metropolis-Hastings 更新：在每一步更新中，通过计算接受概率，将 Potts 模型的先验（相邻标签相同的偏好）和数据的似然性结合起来，决定是否接受新的候选标签。

通过这个过程，Metropolis-Hastings 算法确保了在更新标签时，不仅考虑数据与标签的一致性，还考虑了标签之间的相似性，使得标签配置符合 Potts 模型的先验。

# Spatial clustering model at enhanced resolution

To enhance the resolution of the clustering map, we segmented each spot into subspots and again leveraged spatial information using the potts model spatial prior.

As gene expression is not observed at the subspot level, it is modeled as another latent variable that is also estimated through MCMC. The latent expression of each subspot $j$ that is apart of spot $i$ is denoted as $\gamma_{ij}^{*}$, initialized to be $\gamma_i$ and then updated via the Metropolis-Hastings algorithm.

In each iteration and for each spot, the new proposal is given by $\gamma_{ij}^{*'}=\gamma_{ij}^{*}+\varepsilon_{ij}$ for each subspot, such that the error $\varepsilon_{ij} \thicksim N(0,\sigma^2I_d)$, where $\sigma^2$ is a small fixed parameter and $\sum_j\varepsilon_{ij}=0$ In effect, this jitters the latent expression value of each subspot within a spot while keeping the total expression of the spot fixed.

这里就是讲了一下怎么处理 subspot 里面的数据

# Mapping high-resolution PCs to high-resolution gene expression space

BayesSpace implements two options for predicting high-resolution gene expression: linear regresssion and nonlinear regression using XGBoost(default).

In our analyses, we used the two-sided Wilcoxon rank-sum test as implemented in Seurat to identify the top differentially expressed genes, and also we used Seurat for heatmap visualization of the centered and scaled gene expression values.

这一段就是在说把 PC 的值返回去预测原来的 high-resolution gene expression, 也就是把压缩后的数据解压回去。

# Simulation

解释了一下自己做的实验

# 总结

这文章是真难，比起直接用机器学习模型，这文章的逻辑性更强，可解释性更强，读起来由于全是概率论的知识点可以说是举步维艰。但感觉这才是做科研的样子嘛，直接套用一些莫名其妙的模型，也不知道为什么这样干，这做起来感觉也没劲。

这些找空间域的方法都有个特点，就是先用什么 Louvain、mclust 这种方法先聚一遍类，然后在此基础上进行优化。而优化的方法各有不同，但都是往着自己认定的理想的数据去进行处理。例如 SpaGCN 是对学生 t 分布进行聚类，STAGATE 是利用深度学习进行对周围节点的 embedding，MENDER 是通过不同的分辨率，不同的 scale 再把这些所有的 scale 重新认定为这个点的特征，而这篇文章主要利用了 MCMC method 去让我们聚类的数据满足正态分布（t 分布）的形式，同时结合了 Potts model 让节点能够感知到邻居节点的特征。

但以上的方法都是去寻找邻居，没有从一个全局的角度去把握。当然我之前也想过这个问题，但当时我认为这样做其实没有必要，因为组织的数据应该是一个不断延申的过程，提取周围节点的数据已经足够了。结果在组会听到了一个利用计算机视觉的方法去结合图像数据和 single cell 的数据进行 embedding 的方法，效果奇佳。我想可能就是使用了全局的数据。

总之对于这篇文章阅读完毕了，代码不总结了，R 语言学不来，后面再看吧。